Semi-group algebra
An algebra  over a field
over a field  with a basis
with a basis 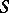 that is at the same time a multiplicative semi-group. In particular, if
that is at the same time a multiplicative semi-group. In particular, if 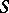 is a group, one obtains a group algebra. If the semi-group
is a group, one obtains a group algebra. If the semi-group  contains a zero, this zero is usually identified with the zero of the algebra
contains a zero, this zero is usually identified with the zero of the algebra  . The problem of describing all linear representations of a semi-group
. The problem of describing all linear representations of a semi-group  over a field
over a field  (cf. Linear representation; Representation of a semi-group) is equivalent to that of describing all representations of the algebra
(cf. Linear representation; Representation of a semi-group) is equivalent to that of describing all representations of the algebra  . The importance of semi-group algebras in the theory of semi-groups is the possibility they offer of utilizing the richer tools of the theory of algebras to study linear representations of semi-groups. An example of this kind of result is: The algebra
. The importance of semi-group algebras in the theory of semi-groups is the possibility they offer of utilizing the richer tools of the theory of algebras to study linear representations of semi-groups. An example of this kind of result is: The algebra 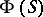 of a finite semi-group
of a finite semi-group 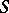 is semi-simple if and only if all linear representations of the semi-group
is semi-simple if and only if all linear representations of the semi-group  over the algebra
over the algebra  are reducible.
are reducible.
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1 , Amer. Math. Soc. (1961) |
Comments
More precisely, let 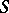 be a semi-group and
be a semi-group and 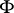 a field. Consider the vector space
a field. Consider the vector space  of all formal finite sums
of all formal finite sums 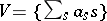 , i.e. the vector space over
, i.e. the vector space over 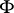 with basis
with basis 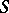 . The semi-group multiplication
. The semi-group multiplication  extends linearly to define an algebra structure on
extends linearly to define an algebra structure on 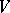 . This is the semi-group algebra
. This is the semi-group algebra 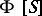 .
.
If 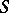 is a semi-group with zero
is a semi-group with zero  , the subspace
, the subspace 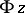 is an ideal in
is an ideal in 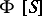 and the contracted semi-group algebra
and the contracted semi-group algebra 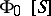 is the quotient algebra
is the quotient algebra 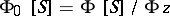 .
.
For an inverse semi-group (cf. Inversion semi-group) one has the following analogue of Maschke's theorem (cf. Group algebra). The semi-group algebra 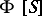 of a finite inverse semi-group
of a finite inverse semi-group 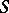 is semi-simple if and only if the characteristic of
is semi-simple if and only if the characteristic of 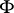 is zero or is a prime that does not divided the order of any sub-semi-group of
is zero or is a prime that does not divided the order of any sub-semi-group of 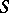 .
.
Semi-group algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-group_algebra&oldid=25733