Additive function

finitely-additive function (on sets, on domains)

A real-valued function 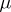defined on a system of sets and such that

(*)

for any finite number of pairwise-disjoint sets 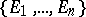of 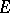whose union also belongs to 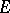. Countably-additive set functions are an important kind of additive functions (cf. Countably-additive set function).

Comments

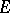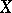Suppose that is a -algebra on a set . Then a non-negative function 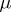(taking, possibly, the value 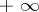) on 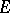is an additive (finitely-additive, countably-additive) measure if it satisfies (*) for an arbitrary (respectively, finite, countable) number of disjoint sets 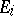in .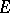

Usually, a measure (sic) is a countably-additive measure.

References

[a1]	H.L. Royden, "Real analysis" , Macmillan (1968)