Cube-like continuum

-cube-like continuum

A compactum (metrizable compactum) admitting, for any 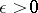, an -mapping onto the ordinary cube 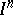. If a compactum 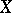is the limit of a countable spectrum of compacta imbeddable in 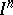, then 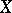is a subset of a cube-like continuum. The class of cube-like continua contains a universal element, i.e. a cube-like continuum 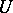such that every cube-like continuum is homeomorphic to some subspace of .

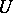References

[1]	B.A. Pasynkov, "On universal compacta" Russian Math. Surveys , 21 : 4 (1966) pp. 77–86 Uspekhi Mat. Nauk , 21 : 4 (1966) pp. 91–100

Comments

In the special case 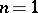, these continua are also called snake-like, see [a1].

In [1] it is shown that a space is 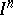-like if and only if it is homeomorphic to the limit of an inverse sequence of copies of 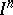with surjective bounding mappings.

References

[a1]	R.H. Bing, "Snake-like continua" Duke Math. J. , 18 (1951) pp. 553–663