Asymptotic density

A variant of the general concept of the density of a sequence of natural numbers; which measures how large a part of the sequence of all natural numbers belongs to the given sequence 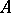of natural numbers including zero. The asymptotic density of a sequence 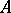is expressed by the real number 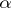defined by the formula

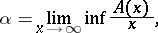where

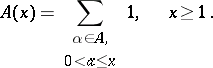The number

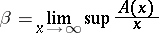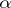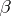is known as the upper asymptotic density. If the numbers and coincide, their common value is called the natural density. Thus, for instance, the sequence of numbers that are free from squares has the natural density 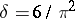. The concept of an asymptotic density is employed in finding criteria for some sequence to be an asymptotic basis.

Comments

The number 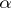as defined above is also called the lower asymptotic density.

References

[a1]	H. Halberstam, K.F. Roth, "Sequences" , 1 , Clarendon Press (1966)