Fabry theorem

Fabry's gap theorem: If the exponents in the power series

with radius of convergence , , 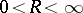satisfy the condition

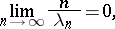then all points of the circle are singular points for . The theorem can be generalized to Dirichlet series.

Fabry's quotient theorem: If the coefficients in the power series

with unit radius of convergence, satisfy the condition

then is a singular point of .

Theorems 1) and 2) were obtained by E. Fabry [1].

References

[1]	E. Fabry, "Sur les points singuliers d'une fonction donée par son développement en série et l'impossibilité du prolongement analytique dans des cas très généraux" Ann. Sci. Ecole Norm. Sup. , 13 (1896) pp. 367–399
[2]	L. Bieberbach, "Analytische Fortsetzung" , Springer (1955)
[3]	A.F. Leont'ev, "Exponential series" , Moscow (1976) (In Russian)

References

[a1]	E. Landau, "Darstellung und Begründung einiger neuerer Ergebnisse der Funktionentheorie" , Das Kontinuum und andere Monographien , Chelsea, reprint (1973)
[a2]	P. Dienes, "The Taylor series" , Oxford Univ. Press & Dover (1957)