Lacunary power series
From Encyclopedia of Mathematics
A series
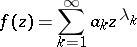 | (*) |
with gaps (lacunas), so that the exponents 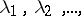 do not run through all the natural numbers. Depending on the properties of the sequence
do not run through all the natural numbers. Depending on the properties of the sequence 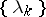 one obtains many properties of the series (*). Thus, if
one obtains many properties of the series (*). Thus, if
 |
and the series (*) converges in the disc  ,
, 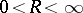 , then all points of the circle
, then all points of the circle 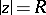 are singular for
are singular for 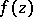 (Hadamard's gap theorem). A strengthening of this theorem is Fabry's gap theorem (cf. Fabry theorem). If the lower density
(Hadamard's gap theorem). A strengthening of this theorem is Fabry's gap theorem (cf. Fabry theorem). If the lower density
 |
then 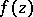 is a single-valued analytic function with simply-connected domain of existence (Pólya's theorem). See also Over-convergence.
is a single-valued analytic function with simply-connected domain of existence (Pólya's theorem). See also Over-convergence.
References
| [1] | L. Bieberbach, "Analytische Fortsetzung" , Springer (1955) pp. Sect. 3 |
Comments
References
| [a1] | E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1979) |
| [a2] | P. Dienes, "The Taylor series" , Oxford Univ. Press & Dover (1957) |
How to Cite This Entry:
Lacunary power series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lacunary_power_series&oldid=24997
Lacunary power series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lacunary_power_series&oldid=24997
This article was adapted from an original article by A.F. Leont'ev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article