Darboux equation
An ordinary differential equation
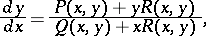 |
where 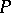 ,
, 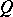 and
and 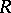 are integral polynomials in
are integral polynomials in  and
and 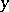 . This equation was first studied by G. Darboux [1]. The Jacobi equation is a special case of the Darboux equation. Let
. This equation was first studied by G. Darboux [1]. The Jacobi equation is a special case of the Darboux equation. Let  be a highest degree of the polynomials
be a highest degree of the polynomials 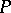 ,
, 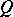 ,
, 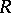 ; if the Darboux equation has
; if the Darboux equation has  known particular algebraic solutions, then if
known particular algebraic solutions, then if 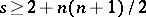 , its general solution is found without quadratures, and if
, its general solution is found without quadratures, and if 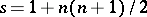 , an integrating factor can be found [2]. If
, an integrating factor can be found [2]. If 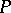 and
and 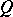 are homogeneous functions of degree
are homogeneous functions of degree  , and
, and 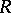 is a homogeneous function of degree
is a homogeneous function of degree 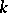 then, if
then, if 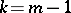 , the Darboux equation is a homogeneous differential equation; if
, the Darboux equation is a homogeneous differential equation; if 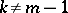 , the Darboux equation may be reduced to a Bernoulli equation by substituting
, the Darboux equation may be reduced to a Bernoulli equation by substituting 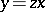 .
.
References
| [1] | G. Darboux, "Mémoire sur les équations différentielles algébriques du premier ordre et du premier degré" Bull. Sci. Math. , 2 (1878) pp. 60–96 |
| [2] | E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) |
N.Kh. Rozov
The hyperbolic equation
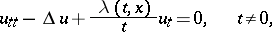 |
where 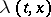 is a non-negative continuously-differentiable function of
is a non-negative continuously-differentiable function of 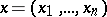 . The following uniqueness theorem is valid both for the solution of the Darboux equation and for the solution of the wave equation. If some twice continuously-differentiable solution
. The following uniqueness theorem is valid both for the solution of the Darboux equation and for the solution of the wave equation. If some twice continuously-differentiable solution 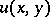 of the Darboux equation vanishes together with its derivative on the base of the characteristic cone lying in the plane
of the Darboux equation vanishes together with its derivative on the base of the characteristic cone lying in the plane 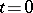 , it vanishes inside the entire domain bounded by this cone. The form of the characteristic cone is the same as for the wave equation. If
, it vanishes inside the entire domain bounded by this cone. The form of the characteristic cone is the same as for the wave equation. If 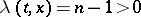 , the solution of the Darboux equation satisfying the initial conditions
, the solution of the Darboux equation satisfying the initial conditions
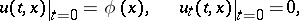 |
with a twice continuously-differentiable function 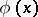 , is the function
, is the function
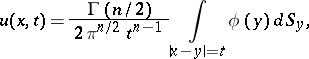 |
where 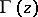 is the gamma-function. This solution of the Darboux equation and the solution
is the gamma-function. This solution of the Darboux equation and the solution 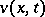 of the wave equation satisfying the conditions
of the wave equation satisfying the conditions
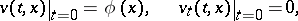 |
are connected by the relation
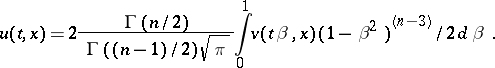 |
The equation was named after G. Darboux.
References
| [1] | F. John, "Plane waves and spherical means applied to partial differential equations" , Interscience (1955) |
Darboux equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_equation&oldid=24848