Arithmetic progression

arithmetic series of the first order

A sequence of numbers in which each term is obtained from the term immediately preceding it by adding to the latter some fixed number 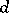, which is known as the difference of this progression. Thus, each arithmetic progression has the form

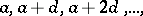in which the general term is

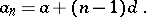A characteristic property of an arithmetic progression is

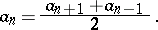If 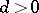, the progression is increasing; if 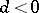, it is decreasing. The simplest example of an arithmetic progression is the series of natural numbers 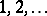. The number of terms of an arithmetic progression can be bounded or unbounded. If an arithmetic progression consists of terms, its sum can be calculated by the formula:

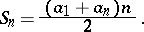Comments

For results on prime numbers in arithmetic progressions see Distribution of prime numbers.