Triangular summation method
From Encyclopedia of Mathematics
A matrix summation method defined by a triangular matrix
 |
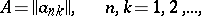that is, by a matrix for which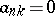 
for 
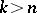. A triangulation summation method is a special case of a row-finite summation method. A triangular matrix 
is called normal if 
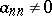for all 
. The transformation
 |
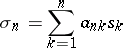realized by a normal triangular matrix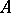 
has an inverse:
 |
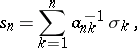where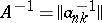 
is the inverse of 
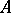. This fact simplifies the proof of a number of theorems for matrix summation methods determined by normal triangular matrices. Related to the triangular summation methods are, e.g., the Cesàro summation methods and the Voronoi summation method.
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [3] | S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian) |
How to Cite This Entry:
Triangular summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Triangular_summation_method&oldid=24809
Triangular summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Triangular_summation_method&oldid=24809
This article was adapted from an original article by I.I. Volkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article