Stirling formula
From Encyclopedia of Mathematics
An asymptotic representation which provides approximate values of the factorials  and of the gamma-function for large values of
and of the gamma-function for large values of  . This representation has the form
. This representation has the form
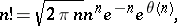 | (*) |
where 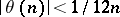 . The asymptotic equalities
. The asymptotic equalities
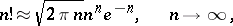 |
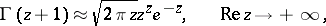 |
hold, and mean that when 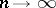 or
or 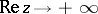 , the ratio of the left- and right-hand sides tends to one.
, the ratio of the left- and right-hand sides tends to one.
The representation (*) was established by J. Stirling (1730).
Comments
See Gamma-function for the corresponding asymptotic series (Stirling series) and additional references.
References
| [a1] | N.G. de Bruijn, "Asymptotic methods in analysis" , Dover, reprint (1981) |
| [a2] | G. Marsaglia, J.C.W. Marsaglia, "A new derivation of Stirling's approximation of 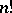 " Amer. Math. Monthly , 97 (1990) pp. 826–829 " Amer. Math. Monthly , 97 (1990) pp. 826–829 |
| [a3] | V. Namias, "A simple derivation of Stirling's asymptotic series" Amer. Math. Monthly , 93 (1986) pp. 25–29 |
How to Cite This Entry:
Stirling formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stirling_formula&oldid=24804
Stirling formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stirling_formula&oldid=24804
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article