Vector field on a manifold

A section of the tangent bundle  . The set of differentiable vector fields forms a module over the ring
. The set of differentiable vector fields forms a module over the ring  of differentiable functions on
of differentiable functions on  .
.
Example 1.
For a chart  of the manifold
of the manifold  one defines the
one defines the  -th basic vector field
-th basic vector field  according to the formula
according to the formula
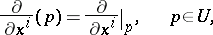 |
where 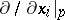 is the
is the 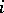 -th basic tangent vector to
-th basic tangent vector to  at the point
at the point 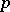 . Any vector field
. Any vector field 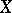 can be uniquely represented in the form
can be uniquely represented in the form
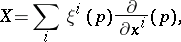 |
where 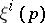 are the components of
are the components of 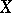 in
in 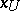 . Since a vector field can be regarded as a derivation of the ring
. Since a vector field can be regarded as a derivation of the ring 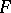 (see example 2), the set of vector fields forms a Lie algebra with respect to the commutation operation (the Lie bracket).
(see example 2), the set of vector fields forms a Lie algebra with respect to the commutation operation (the Lie bracket).
Example 2.
For the chart 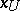 and
and 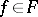 , the function
, the function  is defined by the formula
is defined by the formula
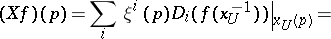 |
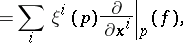 |
where 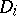 is the partial derivative with respect to
is the partial derivative with respect to 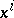 . Note that
. Note that 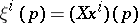 ;
;  is called the derivative of
is called the derivative of 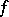 in the direction
in the direction 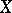 .
.
Example 3.
For the chart  and
and 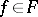 , the commutator (Lie bracket)
, the commutator (Lie bracket)  of the vector fields
of the vector fields
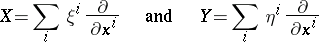 |
is defined by the formula
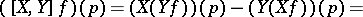 |
 |
It satisfies the relations
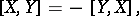 |
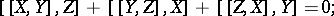 |
in particular,
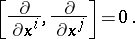 |
Each vector field  induces a local flow on
induces a local flow on 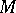 — a family of diffeomorphisms of a neighbourhood
— a family of diffeomorphisms of a neighbourhood 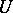 ,
,
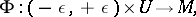 |
such that 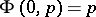 for
for 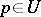 and
and
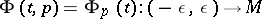 |
is the integral curve of the vector field 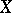 through
through 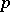 , i.e.
, i.e.
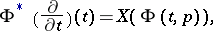 |
where 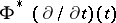 is the tangent vector
is the tangent vector  to
to 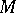 at
at 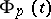 . Conversely, a vector field
. Conversely, a vector field 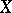 is associated with a local flow
is associated with a local flow 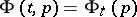 , which is a variation of the mapping
, which is a variation of the mapping 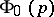 ; here
; here
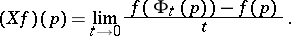 |
Each vector field defines a Lie derivation  of a tensor field of type
of a tensor field of type 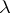 with values in a vector space (infinitesimal transformation of
with values in a vector space (infinitesimal transformation of 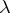 ), corresponding to the local flow
), corresponding to the local flow 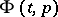 ; its special cases include the action of the vector field on
; its special cases include the action of the vector field on  ,
,
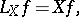 |
and the Lie bracket
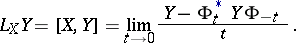 |
A vector field without singularities generates an integrable one-dimensional differential system as well as a Pfaffian system associated with it on 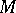 .
.
A generalization of the concept of a vector field on a manifold is that of a vector field along a mapping 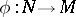 , which is a section of the bundle
, which is a section of the bundle 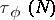 induced by
induced by 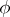 , as well as a tensor field of type
, as well as a tensor field of type 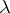 , which is a section of the bundle
, which is a section of the bundle 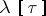 associated with
associated with 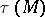 with the aid of the functor
with the aid of the functor 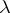 .
.
References
| [1] | C. Godbillon, "Géométrie différentielle et mécanique analytique" , Hermann (1969) |
| [2] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [3] | S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III |
| [4] | K. Nomizu, "Lie groups and differential geometry" , Math. Soc. Japan (1956) |
| [5] | M.M. Postnikov, "Introduction to Morse theory" , Moscow (1971) (In Russian) |
| [6] | S. Helgason, "Differential geometry and symmetric spaces" , Acad. Press (1962) |
Comments
References
| [a1] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
Vector field on a manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector_field_on_a_manifold&oldid=24590