Qualitative theory of differential equations in Banach spaces

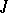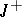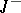A branch of functional analysis in which one studies the behaviour on the real axis or on the positive (or negative) semi-axis (or ) of the solution of the evolution equation in a Banach space. Consider the equations

. ;

. ;

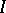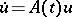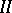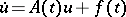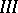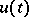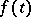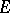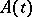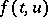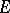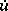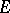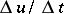. , where is the required function and the given function with values in a complex Banach space ; is a linear operator and is a non-linear operator on . By the derivative one means the limit in the norm of of as .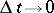

Uniform stability holds for the equation 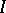if there exists a constant 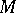such that for any solution 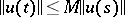, , 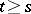and exponential stability if for any solution 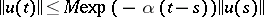for some 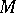and .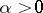

For equation 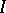with a constant bounded operator 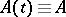, the solution of the Cauchy problem ( 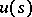given) has the form 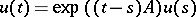. The estimate 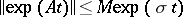holds, where 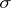is a number greater than the real parts of all points of the spectrum of 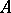. Thus, for exponential stability it is necessary and sufficient that the spectrum of 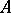lies in the interior of the left half-plane. In a Hilbert space this holds if and only if there exists a positive-definite form 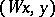for which 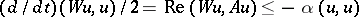for every solution of the equation (Lyapunov's theorem). If the spectrum of 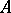is distributed on both sides of the imaginary axis and does not intersect it, then 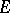can be decomposed into a direct sum of subspaces 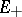and 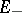which are invariant with respect to 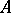, and all the solutions are exponentially increasing (decreasing) in 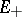(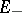) as 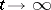. In this case, exponential dichotomy holds for the equation.

If 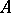is closed, unbounded and has a dense domain in 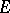, then the Cauchy problem with 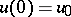is not, in general, well-posed. The existence and properties of the solutions are not determined merely by the distribution of the spectrum of 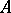; the behaviour of its resolvent 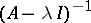must also be specified. Commonly used conditions ensuring the uniform well-posedness of the Cauchy problem on are provided by the inequalities

a sufficient condition for their fulfillment being the Hille–Yosida condition

or the inequality

When these conditions hold, the solution of the Cauchy problem has the form 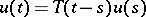, where 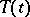is a strongly-continuous semi-group of operators for 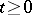and 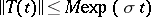. For uniform (or exponential) stability it suffices that 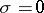(respectively, 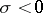). If 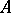generates a strongly-continuous semi-group on a Hilbert space, then the sufficiency part of Lyapunov's theorem holds for it, while if it generates a group, then the necessity part holds as well. In a Hilbert space exponential stability is equivalent to 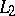-stability, the property that for all solutions .

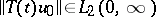Important for applications is the property of almost-periodicity of the solution 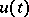or weak almost-periodicity (that is, almost periodicity of the scalar functions 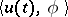for all 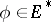). If all values of an almost-periodic solution lie in a compact set, then the solution is compact. Compactness and weak almost-periodicity imply almost-periodicity. For the equation 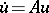, the question of almost-periodicity of the solution is related to the structure of the intersection of the spectrum of 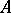with the imaginary axis. If 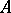is the generating operator of a bounded strongly-continuous semi-group and the above intersection is countable, then for the almost-periodicity of a bounded solution defined on the whole axis it is necessary and sufficient that the limit 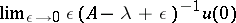exists at each limit point 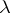of the spectrum on the imaginary axis. Furthermore, each uniformly-continuous solution is weakly almost-periodic; it is almost-periodic if it is weakly compact, or if 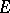contains no subspaces isomorphic to the space 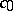of sequences converging to zero, endowed with the max norm. If 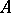is the generating operator of a strongly-continuous semi-group 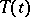with the property that the functions 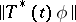are bounded on 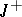for a set of functionals 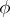which are dense in 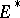, then compactness of a solution implies almost-periodicity.

For equation 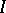with a bounded operator 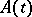that is continuous in 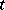, the solutions of the Cauchy problem are defined on the whole axis and, by means of the evolution operator 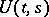, can be written in the form 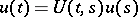. The property of uniform stability is equivalent to the requirement that 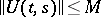; the property of exponential stability is equivalent to 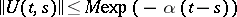. If 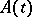is bounded in integral norm, that is, 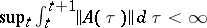, then the general index

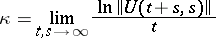is finite. If 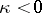, one has exponential stability. For equations with a constant or periodic operator, the formula 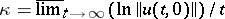holds. It does not hold in the general case. The general index is not altered if 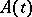is perturbed by adding a term 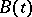for which 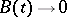as 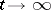, or for which the integral 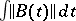converges at infinity. The size of the general index depends on the behaviour of 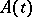at infinity. If the limit 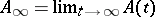exists and the spectrum of lies in the interior of the left half-plane, then 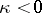. If the operators 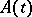, , 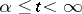form a compact set in the space of bounded operators, if the spectra of all limit operators belong to a half-plane 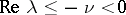and if the operator function 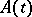has small oscillation, for example, it has the form 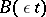for sufficiently small , or if, for sufficiently large 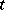, it satisfies the Lipschitz condition 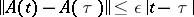with sufficiently small, then 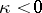. In a Hilbert space the condition 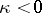is equivalent to the existence of a Hermitian form 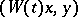such that 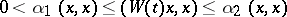and 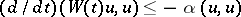for every solution .

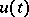If 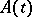is periodic with period 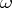, i.e. if 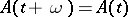, then 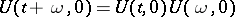. The operator 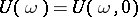is called the monodromy operator of equation 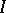. Its spectral radius 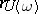is related to the general index by the formula 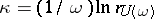. The equation has a periodic solution if and only if 1 is an eigen value of 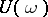. If the operator 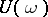has a logarithm, then the Floquet representation 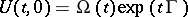holds, where 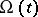is periodic with perio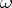d and 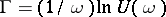. In particular, the Floquet representation holds if the spectrum of 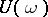does not surround the origin; and for this it suffices that 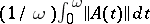be less than a certain constant, which depends on the geometry of the sphere in 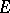and which is not less than 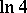. For Hilbert space this constant is 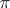. The Floquet representation reduces the question of the behaviour of the solution of the equation to the same question for the equation 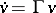with a constant operator .

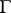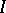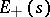Exponential dichotomy holds for equation if for some the space decomposes into a direct sum of subspaces and 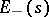such that

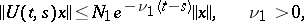when 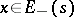, , 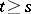and

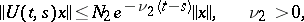when 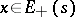, 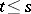. It is supposed here that the subsequences 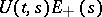and are, in a certain sense, not close to each other. If the general index is finite, this latter requirement holds automatically. For an equation with a periodic 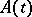, a necessary and sufficient condition for exponential dichotomy to hold is that the spectrum of the monodromy operator be distributed outside and inside the unit disc without intersecting the unit circle.

For equation 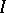with an unbounded operator 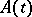whose domain does not depend on 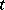and which satisfies the well-posedness conditions for the Cauchy problem (see above) for every 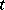, the existence of an evolution operator 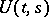, defined and strongly continuous in and for 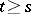, has been proved, under supplementary smoothness conditions. This enables one to carry over to this case a number of the ideas and results described above. However, some difficulties are encountered. E.g., the Floquet representation can be obtained only in a Hilbert space when 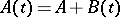, where 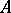is a negative-definite self-adjoint operator and 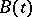is a bounded periodic operator satisfying certain extra conditions.

Suppose that 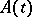is periodic and that the Cauchy problem for equation 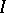is uniformly well-posed. If the intersection of the spectrum of the monodromy operator 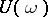with the unit circle is countable, then each bounded uniformly-continuous solution on 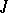is weakly almost-periodic. It is almost-periodic in the case of weak compactness or if 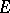does not contain 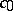. A reflexive space 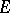admits a direct sum decomposition 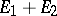such that 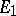and 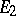are invariant with respect to 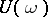and all the solutions starting in 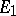are almost-periodic, while those starting in 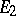are in a certain sense decreasing: For , ,

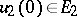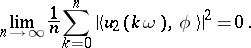For the solution of the non-homogeneous equation , the following formula holds:

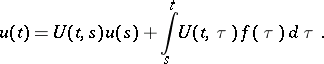For an equation with a bounded operator, this equation is equivalent to the differential equation. In the case of an unbounded operator, this is generally not so, but then this equation is taken as the definition of the (generalized) solution. The fundamental problem for equation 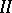is to investigate the properties of the solutions under prescribed properties of the right-hand side. These properties are usually described in terms of the function 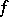belonging to some Banach space of functions on 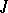or 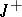with values in 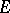. If corresponding to each bounded continuous function 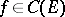there is at least one bounded solution, then the operator 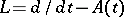is called weakly regular. If corresponding to each 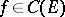there is a unique solution 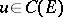, then 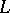is called regular. For bounded constant 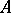, weak regularity implies regularity. This assertion is no longer true for unbounded 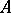or for bounded periodic 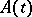, even in a Hilbert space. If the general index of the equation 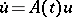is finite, then exponential dichotomy for this equation is equivalent to regularity of 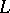on . 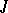For exponential dichotomy to hold on 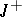it is necessary and sufficient that 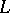be weakly regular on 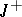and that the set of those initial values 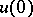to which the bounded solutions of equation 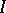correspond be a complemented subspace of 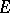. If for all solutions of 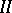the inequality

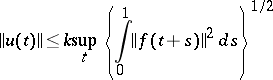holds, and if for the solution of the formal adjoint equation 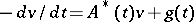the inequality 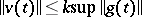holds, then the operators 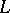and 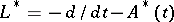are regular. It is not known (1990) whether regularity is preserved on replacing the right-hand side of the first inequality by 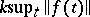. For the regularity of 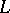and 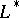both, a priori estimates are necessary.

If 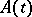is periodic, then a necessary and sufficient condition for the existence of periodic solutions for each periodic 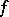is that the mapping 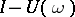be surjective, while for such a solution to be unique, it is necessary and sufficient that the operator 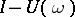be invertible.

The verification of regularity under known conditions can be reduced to the verification of the regularity of operators with constant coefficients. In the case when is strongly oscillating (for example 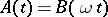with 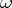large), under the assumption that the mean

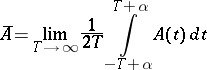exists uniformly with respect to 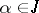, the operator 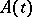is regular if and only if the operator 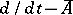is regular.

For almost-periodic solutions the specifics of an infinite-dimensional space are already encountered in a generalization of the well-known Bohl–Bohr theorem on the almost-periodicity of a bounded integral of an almost-periodic function, that is, on the almost-periodicity of a solution of the simplest differential equation 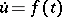. 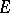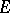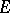If the indefinite integral of an almost-periodic function with values in is bounded in and does not contain 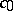, then the function is almost-periodic. The Bohl–Bohr theorem fails in 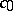. 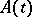If is periodic, 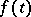is almost-periodic and the intersection of the spectrum of the monodromy operator 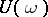with the unit circle is countable, then the same conclusions on the almost-periodicity of solutions stated earlier for the homogeneous equation hold for this case. If 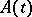is almost-periodic (as a function with values in the space of bounded operators on 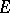), then in order that for each almost-periodic function 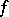there exists a unique almost-periodic solution, it is necessary and sufficient that 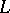be regular. If equation 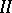has a (weakly) compact solution for 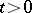, and the non-trivial (weakly) compact solutions of the homogeneous equation 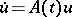have the property that 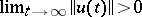, then equation 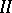has a (weakly) almost-periodic solution.

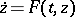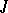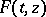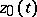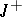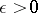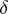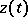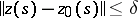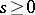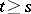In the qualitative study of a non-linear equation , it is usually supposed in advance that conditions hold which ensure that solutions exist on or on ; this imposes an essential constraint on the form of non-linearity of . A solution on is said to be uniformly stable if there exists for each a such that for every other solution the inequality , , implies that is defined for and that 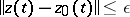. A solution is called asymptotically stable if it is uniformly stable and if for some 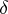the inequality 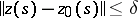implies that 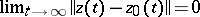. If one makes the substitution 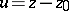in the equation, then after linearization (if this is possible) it takes the form 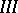, where 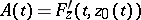, and the non-linearity has the property that 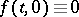. Thus the problem of uniform (asymptotic) stability of the solution reduces to that of the uniform (or asymptotic) stability of the zero solution of 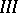. In this connection, the equation 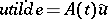is called the linearization equation (or variational equation) of the original equation with respect to the solution .

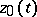If the non-linear part 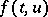is sufficiently small, then the properties of the solutions are determined by those of the linearized equation. If the general index of the linearized equation is negative and the inequality 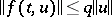, , 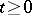, 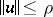holds, then for sufficiently small 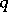the zero solution of 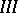is asymptotically stable. If 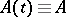and the spectrum of 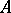does not intersect the imaginary axis and has a point in the right half-plane, then for sufficiently small 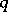the zero solution is unstable. If the inequality

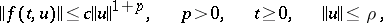holds, then the requirement that there be no points of the spectrum on the imaginary axis can be deleted.

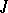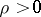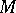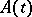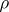If exponential dichotomy holds on for the linearized equation, then for every there exist and depending on and such that the inequalities

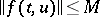and

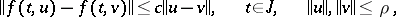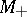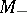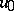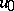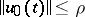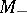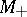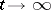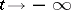imply the existence, in some neighbourhood of the origin, of two manifolds and , intersecting at the single point , such that the solution starting at is bounded on the entire axis and ; solutions starting on () approach exponentially as () and move away from it as 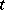goes to infinity in the opposite direction. Furthermore, 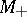(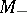) is homeomorphic to the neighbourhood of the space 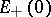(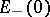) involved in the definition of exponential dichotomy. If under the above conditions 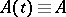and 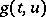is almost-periodic in 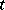for each with 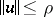, then the solution is almost-periodic.

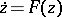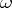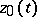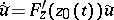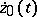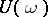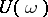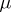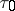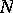Suppose that the autonomous equation has an -periodic solution ; then the linearized equation has a single periodic solution and, consequently, its monodromy operator has 1 as eigen value. If this eigen value is simple and the remaining spectrum of lies in the interior of the unit disc and does not surround the origin, then there exist numbers , and such that 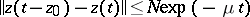for all other solutions of the original equation. This property is called asymptotic orbital stability of the periodic solution. Studies have also been made of other stable invariant manifolds for non-linear equations.

Equations of type 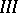with an unbounded operator 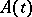correspond in applications to quasi-linear equations of parabolic or hyperbolic type. A theory of "properly" non-linear equations of a specific type has been developed. Thus, if 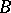is a continuous everywhere-defined dissipative operator, then the Cauchy problem 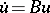, , is uniquely solvable on the semi-axis 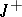for any 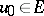. The definition of a dissipative operator carries over in a natural fashion to the case of a many-valued operator; for such operators one considers a differential inclusion 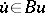rather than a differential equation. If on a reflexive space 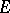, the operator 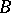is closed and dissipative and if the values of 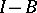cover the entire space 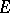, then the Cauchy problem is uniquely solvable on 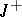for each 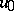in the domain of 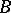. There are many variants of the latter statement. The solution is given by the formula 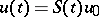, where 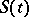is a semi-group of non-linear operators, , 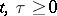. For equations with dissipative operators there are also existence theorems for periodic and almost-periodic solutions.

References

[1]	Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian)
[2]	H.H. Schaefer, "Linear differential equations and function spaces" , Acad. Press (1966)
[3]	K. Yosida, "Functional analysis" , Springer (1968)
[4]	S.G. Krein, "Linear differential equations in Banach space" , Transl. Math. Monogr. , 29 , Amer. Math. Soc. (1971) (Translated from Russian)
[5]	V. Barbu, "Nonlinear semigroups and differential equations in Banach spaces" , Ed. Academici (1976) (Translated from Rumanian)
[6]	A.G. Baskakov, "On the spectral analysis of isometric representations of locally compact Abelian groups" Trudy Mat. Fak. Vorozhen. Inst. , 10 (1973) pp. 96–101 (In Russian)
[7]	V.V. Zhikov, "Some admissibility and dichotomy questions. The averaging principle" Math. USSR Izv. , 10 (1976) pp. 1307–1332 Izv. Akad. Nauk SSSR Ser. Mat. , 40 : 6 (1976) pp. 1380–1408
[8]	V.V. Zhikov, B.M. Levitan, "Favard theory" Russian Math. Surveys , 32 : 2 (1977) pp. 129–180 Uspekhi Mat. Nauk , 32 : 2 (1977) pp. 123–171
[9]	A.I. Miloslavskii, "Floquet theory for parabolic equations" Funct. Anal. Appl. , 10 : 2 (1976) pp. 151–153 Funktsional. Anal. i Prilozhen. , 10 : 2 (1976) pp. 80–81
[10]	V.M. Tyurin, "Functional analysis" , 1 , Ul'yanovsk (1973) (In Russian)
[11]	B.M. Levitan, V.V. Zhikov, "Almost-periodic functions and differential equations" , Cambridge Univ. Press (1982) (Translated from Russian)

Comments

For a somewhat different approach to the qualitative theory of abstract differential equations see [a1], [a2].

References

[a1]	J.K. Hale, "Asymptotic behavior of dissipative systems" , Amer. Math. Soc. (1988)
[a2]	J.K. Hale, L.T. Magalhes, W.M. Oliva, "An introduction to infinite dimensional dynamical systems" , Springer (1984)