A formula from the restricted predicate calculus having the form
where 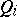 denotes the universal quantifier
denotes the universal quantifier 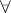 or the existential quantifier
or the existential quantifier 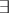 , the variables
, the variables 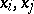 are distinct for
are distinct for 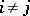 , and
, and 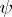 is a formula without quantifiers. Prenex formulas are also called prenex normal forms or prenex forms.
is a formula without quantifiers. Prenex formulas are also called prenex normal forms or prenex forms.
For each formula 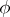 of the language of the restricted predicate calculus there is a prenex formula that is logically equivalent to
of the language of the restricted predicate calculus there is a prenex formula that is logically equivalent to 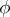 in the classical predicate calculus. The procedure of finding a prenex formula is based on the following equivalences, which can be deduced in the classical predicate calculus:
in the classical predicate calculus. The procedure of finding a prenex formula is based on the following equivalences, which can be deduced in the classical predicate calculus:
where 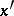 is any variable not appearing as a free variable in
is any variable not appearing as a free variable in 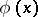 or
or  , and
, and 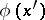 can be obtained from
can be obtained from 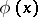 by changing all free appearances of
by changing all free appearances of  to
to 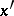 ; the variable
; the variable 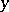 does not appear as a free variable in
does not appear as a free variable in 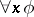 or
or 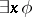 . To use the above equivalences one has to first express all logical operators by
. To use the above equivalences one has to first express all logical operators by 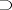 and
and  and then move all quantifiers to the left by applying the equivalences. The prenex formula thus obtained is called the prenex form of the given formula.
and then move all quantifiers to the left by applying the equivalences. The prenex formula thus obtained is called the prenex form of the given formula.
References
| [1] | E. Mendelson, "Introduction to mathematical logic" , v. Nostrand (1964) |
References
| [a1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1950) pp. Chapt. VII, §35 |
| [a2] | R. Fraissé, "Course of mathematical logic" , 1 , Reidel (1973) pp. Sect. 5.1.1ff |
How to Cite This Entry:
Prenex formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Prenex_formula&oldid=24538
This article was adapted from an original article by V.N. Grishin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article
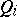 denotes the universal quantifier
denotes the universal quantifier 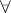 or the existential quantifier
or the existential quantifier 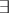 , the variables
, the variables 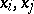 are distinct for
are distinct for 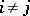 , and
, and 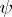 is a formula without quantifiers. Prenex formulas are also called prenex normal forms or prenex forms.
is a formula without quantifiers. Prenex formulas are also called prenex normal forms or prenex forms.
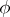 of the language of the restricted predicate calculus there is a prenex formula that is logically equivalent to
of the language of the restricted predicate calculus there is a prenex formula that is logically equivalent to 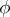 in the classical predicate calculus. The procedure of finding a prenex formula is based on the following equivalences, which can be deduced in the classical predicate calculus:
in the classical predicate calculus. The procedure of finding a prenex formula is based on the following equivalences, which can be deduced in the classical predicate calculus:
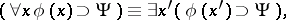
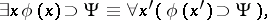
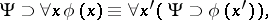
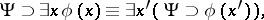


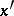 is any variable not appearing as a free variable in
is any variable not appearing as a free variable in 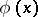 or
or  , and
, and 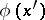 can be obtained from
can be obtained from 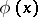 by changing all free appearances of
by changing all free appearances of  to
to 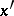 ; the variable
; the variable 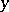 does not appear as a free variable in
does not appear as a free variable in 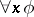 or
or 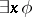 . To use the above equivalences one has to first express all logical operators by
. To use the above equivalences one has to first express all logical operators by  and
and  and then move all quantifiers to the left by applying the equivalences. The prenex formula thus obtained is called the prenex form of the given formula.
and then move all quantifiers to the left by applying the equivalences. The prenex formula thus obtained is called the prenex form of the given formula.