Papperitz equation
An ordinary second-order Fuchsian linear differential equation having precisely three singular points:
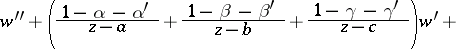 | (1) |
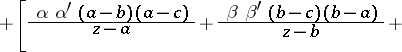 |
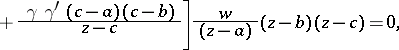 |
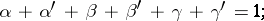 |
here  are pairwise distinct complex numbers,
are pairwise distinct complex numbers,  (
( and
and  ) are the characteristic exponents at the singular point
) are the characteristic exponents at the singular point  (respectively,
(respectively, 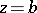 and
and  ). A Papperitz equation is uniquely determined by the assignment of the singular points and the characteristic exponents. In solving a Papperitz equation (1), use is made of Riemann's notation:
). A Papperitz equation is uniquely determined by the assignment of the singular points and the characteristic exponents. In solving a Papperitz equation (1), use is made of Riemann's notation:
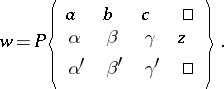 |
B. Riemann investigated [1] the problem of finding all many-valued functions  , analytic in the extended complex plane, which have the following properties:
, analytic in the extended complex plane, which have the following properties:
a) the function 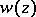 has precisely three singular points
has precisely three singular points 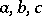 ;
;
b) any three of its branches are connected by a linear equation
 |
with constant coefficients;
c) the function 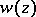 has the simplest singularities at the points
has the simplest singularities at the points  ; namely, in a neighbourhood of the point
; namely, in a neighbourhood of the point  there are two branches
there are two branches 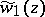 and
and  satisfying
satisfying
 |
where 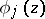
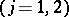 is holomorphic at
is holomorphic at  ; and analogously for
; and analogously for 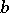 and
and  .
.
Riemann, under certain additional assumptions on the numbers 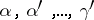 , showed that all such functions can be expressed in terms of hypergeometric functions and that
, showed that all such functions can be expressed in terms of hypergeometric functions and that 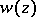 satisfies a linear second-order differential equation with rational coefficients, but did not write this equation out explicitly (see [1]). The equation in question, (1), was given by E. Papperitz [2]. It is also called the Riemann
satisfies a linear second-order differential equation with rational coefficients, but did not write this equation out explicitly (see [1]). The equation in question, (1), was given by E. Papperitz [2]. It is also called the Riemann 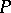 -equation, the Riemann equation in Papperitz's form and the Riemann equation, and its solutions are called
-equation, the Riemann equation in Papperitz's form and the Riemann equation, and its solutions are called 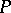 -functions.
-functions.
The basic properties of the solutions of a Papperitz equation are as follows.
1) A Papperitz equation is invariant under rational-linear transformations: If 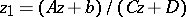 maps the points
maps the points 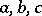 to points
to points 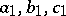 , then
, then
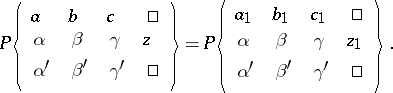 |
2) The transformation
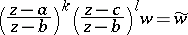 |
transforms a Papperitz equation into a Papperitz equation with the same singular points, but with different characteristic exponents:
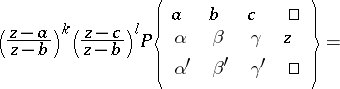 |
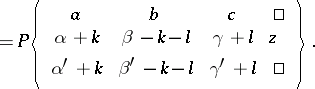 |
3) The hypergeometric equation
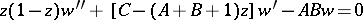 |
is a special case of a Papperitz equation and it corresponds in Riemann's notation to
 |
4) Each solution of a Papperitz equation can be expressed in terms of the hypergeometric function,
 | (2) |
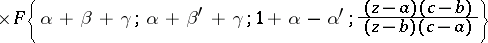 |
under the assumption that 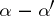 is not a negative integer. If none of the differences
is not a negative integer. If none of the differences 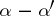 ,
, 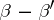 ,
, 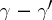 are integers, then interchanging in (2) the positions of
are integers, then interchanging in (2) the positions of  and
and  or of
or of 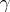 and
and 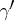 , four solutions of a Papperitz equation are obtained. In addition a Papperitz equation remains unchanged if the positions of the triples
, four solutions of a Papperitz equation are obtained. In addition a Papperitz equation remains unchanged if the positions of the triples  ,
, 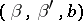 ,
, 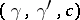 are rearranged; all these rearrangements provide 24 special solutions of a Papperitz equation (1), which were first obtained by E.E. Kummer [5].
are rearranged; all these rearrangements provide 24 special solutions of a Papperitz equation (1), which were first obtained by E.E. Kummer [5].
References
| [1] | B. Riemann, "Beiträge zur Theorie der durch Gauss'sche Reihe  darstellbare Functionen" , Gesammelte math. Werke , Dover, reprint (1953) pp. 67–85 darstellbare Functionen" , Gesammelte math. Werke , Dover, reprint (1953) pp. 67–85 |
| [2] | E. Papperitz, "Ueber verwandte  -Functionen" Math. Ann. , 25 (1885) pp. 212–221 -Functionen" Math. Ann. , 25 (1885) pp. 212–221 |
| [3] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 |
| [4] | V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) |
| [5] | E.E. Kummer, "Ueber die hypergeometrische Reihe  " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 |
Papperitz equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Papperitz_equation&oldid=24524