K-contact-flow

A contact form on a smooth -dimensional manifold is a -form such that is everywhere non-zero. The pair is called a contact manifold. See also Contact structure.

A contact manifold carries a distinguished vector field , called the characteristic vector field or Reeb field, which is uniquely determined by the following equations: and for all vector fields . The flow 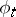generated by (when it is complete) is called the contact flow. Sometimes the name "contact flow" is used for the -dimensional foliation consisting of the unparametrized orbits of 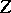, [a5].

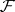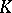If the flow is a Riemannian foliation in the sense of Reinhart–Molino [a7], i.e., if there is a holonomy-invariant transverse metric for , then is called a -contact flow, and the pair 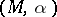is called a -contact manifold. 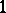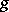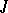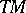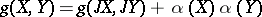This definition is equivalent to requiring that the flow of is a -parameter group of isometries for some contact metric (a Riemannian metric such that there exists an endomorphism of the tangent bundle such that , , , and for all vector fields 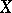and on ). If one has in addition 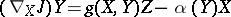, where is the Levi-Civita connection of 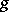, then one says that 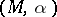is a Sasakian manifold, [a4], [a12].

As a consequence of the Meyer–Steenrod theorem [a6], a 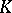-contact flow 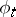on a compact -dimensional manifold is almost periodic: the closure of 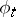in the isometry group of 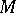(of the associated contact metric) is a torus , of dimension 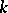in between 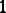and 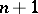, which acts on 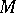while preserving the contact form 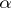, [a3]. The "completely integrable" case 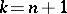has been studied in [a2]: these structures are determined by the image of their contact moment mapping.

The existence of 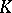-contact flows poses restrictions on the topology of the manifold. For instance, since a -contact flow can be approximated by a periodic -contact flow, only Seifert fibred compact manifolds can carry a 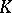-contact flow. Another example of a restriction is the Tachibana theorem, asserting that the first Betti number of a compact Sasakian manifold is either zero or even, [a9]. This shows that no torus can carry a Sasakian structure. Actually, P. Rukimbira [a8] showed that no torus can carry a 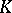-contact flow.

A. Weinstein [a11] has conjectured that the contact flow of a compact contact manifold has at least one periodic orbit. Despite important breakthroughs (including [a10]), this conjecture is not quite settled at present (1996). However, it is known that -contact flows on compact manifolds have at least two periodic orbits [a3].

Examples of 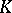-contact manifolds include the contact manifolds with a periodic contact flow (these include the regular contact manifolds), such as the sphere 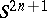equipped with the contact form 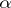that is the restriction to 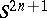of the 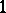-form

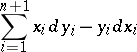on 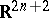. More generally, compact contact hypersurfaces (in the sense of M. Okumura) [a1] in Kähler manifolds of constant positive holomorphic sectional curvature carry 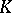-contact flows. A large set of examples is provided by the Brieskorn manifolds: In [a12] it is shown that every Brieskorn manifold admits many Sasakian structures, hence carries many -contact flows.

References

[a1]	A. Banyaga, "On characteristics of hypersurfaces in symplectic manifolds" , Proc. Symp. Pure Math. , 54 , Amer. Math. Soc. (1993) pp. 9–17
[a2]	A. Banyaga, P. Molino, "Complete integrability in contact geometry" , Memoirs , Amer. Math. Soc. (submitted)
[a3]	A. Banyaga, P. Rukimbira, "On characteristics of circle invariant presymplectic forms" Proc. Amer. Math. Soc. , 123 (1995) pp. 3901–3906
[a4]	D.E. Blair, "Contact manifolds in Riemannian geometry" , Lecture Notes in Mathematics , 509 , Springer (1976)
[a5]	Y. Carrière, "Flots riemanniens" Astérisque , 116 (1982) pp. 31–52
[a6]	S.B. Meyer, N.E. Steenrod, "The group of isometries of a Riemannian manifold" Ann. of Math. , 40 (1939) pp. 400–416
[a7]	P. Molino, "Riemannian foliations" , Progress in Math. , Birkhäuser (1984)
[a8]	P. Rukimbira, "Some remarks on 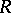-contact flows" Ann. Global Anal. and Geom. , 11 (1993) pp. 165–171
[a9]	S. Tachibana, "On harmonic tensors in compact sasakian spaces" Tohoku Math. J. , 17 (1965) pp. 271–284
[a10]	C. Viterbo, "A proof of the Weinstein conjecture for 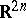" Ann. Inst. H. Poincaré. Anal. Non-Lin. , 4 (1987) pp. 337–356
[a11]	A. Weinstein, "On the hypothesis of Rabinowicz' periodic orbit theorem" J. Diff. Geom. , 33 (1978) pp. 353–358
[a12]	K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984)