Euler-Lagrange equation

for a minimal surface

The equation

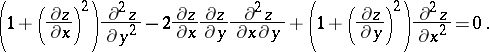It was derived by J.L. Lagrange (1760) and interpreted by J. Meusnier as signifying that the mean curvature of the surface 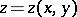is zero. Particular integrals for it were obtained by G. Monge. The Euler–Lagrange equation was systematically investigated by S.N. Bernshtein, who showed that it is a quasi-linear elliptic equation of order 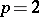and that, consequently, its solutions have a number of properties that distinguish them sharply from those of linear equations. Such properties include, for example, the removability of isolated singularities of a solution without the a priori assumption that the solution is bounded in a neighbourhood of the singular point, the maximum principle, which holds under the same conditions, the impossibility of obtaining a uniform a priori estimate for 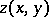in an arbitrary compact subdomain of a disc in terms of the value of at the centre of the disc (that is, the absence of an exact analogue of Harnack's inequality), facts relating to the Dirichlet problem, the non-existence of a non-linear solution defined in the entire plane (the Bernstein theorem), etc.

The Euler–Lagrange equation can be generalized with respect to the dimension: The equation corresponding to a minimal hypersurface 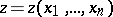in 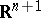has the form

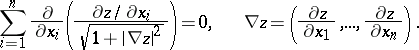For this equation 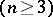the solvability of the Dirichlet problem has been studied, the removability of the singularities of a solution, provided that they are concentrated inside the domain on a set of zero 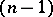-dimensional Hausdorff measure, has been proved, and the validity of Bernstein's theorem for 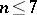and the existence of counter-examples for 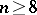has been proved.

Comments

For Bernshtein's paper see [a3].

References

[a1]	E. Giusti, "Minimal surfaces and functions of bounded variation" , Birkhäuser (1984)
[a2]	J.C.C. Nitsche, "Vorlesungen über Minimalflächen" , Springer (1975) pp. §455
[a3]	S.N. [S.N. Bernshtein] Bernstein, "Sur les surfaces définies au moyen de leur courbure moyenne ou totale" Ann. Sci. Ecole Norm. Sup. , 27 (1910) pp. 233–256
[a4]	E. Bombieri, E. Degiorgi, E. Giusti, "Minimal cones and the Bernstein problem" Inv. Math. , 7 (1969) pp. 243–268