Regular singular point

A notion in the theory of ordinary linear differential equations with an independent complex variable. A point 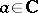is called a regular singular point of the equation

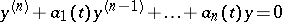(1)

or of the system

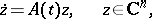(2)

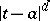with analytic coefficients, if is an isolated singularity of the coefficients and if every solution of (1) or (2) increases no faster than for some , as 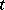tends to within an arbitrary acute angle with vertex . This last restriction is necessary in view of the fact that in a neighbourhood of a regular singular point the solutions are non-single-valued analytic functions, and as 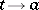along an arbitrary curve, they can increase essentially faster than they do when over a ray with vertex .

For a singular point of the coefficients of (1) or (2) to be a regular singular point of (1) or (2), it must be a pole (of a function), and not an essential singular point, of the coefficients. For equation (1) there is Fuchs' condition: The singular point 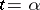of the coefficients 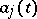of equation (1) is a regular singular point of (1) if and only if the functions 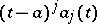, , 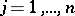are holomorphic at zero. In the case of the system (2) there is the following sufficient condition: If the entries of the matrix 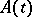have a simple pole at a point , then this point is a regular singular point of (2).

References

[1]	V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian)
[2]	E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17
[3]	A.H.M. Levelt, "Hypergeometric functions I-IV" Proc. Koninkl. Nederl. Akad. Wet. Ser. A , 64 : 4 (1961) pp. 362–403
[4]	P. Deligne, "Equations différentielles à points singuliers réguliers" , Lect. notes in math. , 163 , Springer (1970)
[5]	J. Plemelj, "Problems in the sense of Riemann and Klein" , Wiley (1964)
[6]	V.I. Arnol'd, Yu.S. Il'yashenko, "Ordinary differential equations" , Encycl. Math. Sci. , 1 , Springer (Forthcoming) (Translated from Russian)

Comments

Any second-order equation (1) with three regular singular points can be reduced to the hypergeometric equation. In the case of four regular singular points it can be reduced to Heun's equation [a1], Sect. 15.3, which includes an algebraic form of the Lamé equation. Extensions of the concept to systems of partial differential equations are mentioned in (the editorial comments to) Hypergeometric equation.

References

[a1]	H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 3. Automorphic functions , McGraw-Hill (1955)