Banach algebra

$ \newcommand{\C}{\mathbf{C}} \newcommand{\norm}[1]{\left\|#1\right\|} \newcommand{\abs}[1]{\left|#1\right|} $ A topological algebra $A$ over the field of complex numbers whose topology is defined by a norm which converts $A$ into a Banach space, the multiplication of the elements being separately continuous for both factors. A Banach algebra is said to be commutative if $xy=yx$ for all $x$, $y\in A$ (cf. Commutative Banach algebra). A Banach algebra is said to be an algebra with a unit if $A$ contains an element $e$ such that $ex=xe=x$ for any $x\in A$. If a Banach algebra has no unit, a unit may be adjoined, i.e. it is possible to construct a Banach algebra $\tilde{A}$ with a unit element such that $\tilde{A}$ contains the initial algebra $A$ as a closed subalgebra of codimension one. In any Banach algebra $A$ with a unit element $e$ it is possible to change the norm for an equivalent one so that in the new norm the relationships $\norm{ab} \leq \norm{a}\norm{b}$, $\norm{e} = 1$ are valid. In what follows it is, as a rule, assumed that the algebra does contain a unit and that it satisfies the norm conditions given above.

Examples.

1) Let $X$ be a compact topological space and let $C(X)$ be the set of all continuous complex-valued functions on $X$. $C(X)$ will then be a Banach algebra with respect to the usual operations, with norm $$ \norm{f} = \max_{X}\abs{f}. $$

2) The set of all bounded linear operators on a Banach space forms a Banach algebra with respect to the usual operations of addition and multiplication of linear operators with the operator norm.

3) Let $V$ be a bounded domain in $n$-dimensional complex space $\C^n$. The set of bounded holomorphic functions on $V$ is a Banach algebra with respect to the usual operations, with the natural sup-norm: $$ \norm{f} = \sup_V\abs{f}. $$ This Banach algebra contains the closed subalgebra of bounded holomorphic functions on $V$ that have a continuous extension to the closure of $V$. The simplest example is the algebra of functions that are continuous in the disc $\abs{z} \leq 1$ and analytic in the disc $\abs{z} < 1$.

4) Let $G$ be a locally compact group and let $L_1(G)$ be the space (of equivalence classes) of all functions that are measurable with respect to the Haar measure on $G$ and that are absolutely integrable with respect is this measure, with norm $$ \newcommand{\groupint}[3]{\int_#1 #2\,d#3} \newcommand{\Gint}[1]{\groupint{G}{#1}{g}} \norm{f} = \Gint{\abs{f(g)}} $$ (left Haar integral).

If the convolution operation $$ (f_1 * f_2)(h) = \Gint{f_1(g)f_2(g^{-1}h)} $$ is considered as the multiplication in $L_1(G)$, then $L_1(G)$ becomes a Banach algebra; if $G$ is an Abelian locally compact group, then the Banach algebra $L_1(G)$ is commutative. The Banach algebra $L_1(G)$ is said to be the group algebra of $G$. The group algebra $L_1(G)$ has a unit (with respect to the convolution) if and only if $G$ is discrete.

If 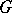is commutative it is possible to construct a faithful representation of 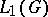, given by the Fourier transform of each function , i.e. by the function

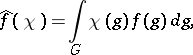on the character group 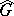of 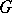. The set of functions 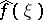forms a certain algebra 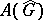of continuous functions on 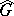(with respect to the ordinary pointwise operations), called the Fourier algebra of the locally compact Abelian group 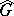. In particular, if 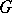is the group of integers 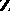, then 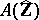is the algebra of continuous functions on the circle which are expandable into an absolutely convergent trigonometric series.

5) Let 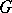be a topological group. A continuous complex-valued functi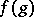on on 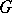is said to be almost periodic if the set of its shifts 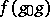, , 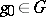forms a compact family with respect to uniform convergence on 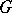. The set of almost-periodic functions forms a commutative Banach algebra with respect to the pointwise operations, with norm

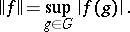6) The skew-field of quaternions does not form a Banach algebra over the field of complex numbers, since the product of elements of a Banach algebra 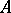should be compatible with multiplication by numbers: For all 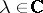and 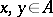the equation

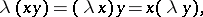must be valid; it is not valid in the field of quaternions if , , .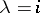

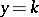Any Banach algebra with a unit is a topological algebra with continuous inverses. Moreover, if 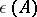is the set of elements of a Banach algebra 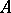which have a (two-sided) inverse with respect to multiplication, then 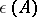is a topological group in the topology induced by the imbedding 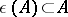. If 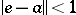, then 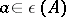, and

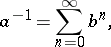where 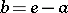, and the series is absolutely convergent. The set of elements invertible from the right (from the left) in 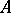also forms an open set in .

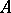If in a Banach algebra 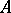all elements have an inverse (or even a left inverse), then 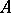is isometrically isomorphic to the field of complex numbers (the Gel'fand–Mazur theorem).

Since a certain neighbourhood of the unit in a Banach algebra 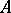consists of invertible elements, the closure of any non-trivial ideal is again an ideal which does not coincide with 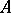. In particular, a maximal (left, right, two-sided) ideal is closed.

An important task in the theory of Banach algebras is the description of closed ideals in Banach algebras. The problem can be simply solved in a number of cases. In the algebra 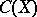(cf. Example 1) each closed ideal has the form 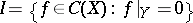, where 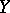is a closed set in 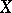. If 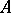is the algebra of all bounded linear operators on a separable infinite-dimensional Hilbert space, then the ideal of completely-continuous operators is the only closed two-sided ideal in .

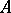An element 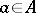has a left (right) inverse if and only if it is not contained in any maximal left (right) ideal. The intersection of all maximal left ideals in 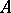coincides with the intersection of all maximal right ideals; this intersection is called the radical of the algebra 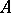and is denoted by 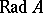. An element 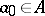belongs to 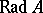if and only if 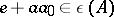for any 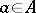. Algebras for which 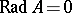are said to be semi-simple. The algebras 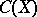and the group algebras 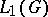are semi-simple. All irreducible (i.e. not having a non-trivial invariant subspace) closed subalgebras of the algebra of all bounded linear operators on a Banach space are semi-simple.

The resolvent of an element 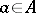is the function

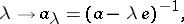defined on the set of all 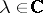for which a (two-sided) inverse to 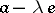exists. The domain of existence of the resolvent contains all points 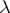with 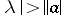. The maximal domain of existence of the resolvent is an open set; the resolvent is continuous on this set and is even analytic, moreover 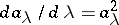. In addition, Hilbert's identity

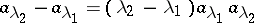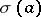is valid. The complement of the domain of existence of the resolvent is called the spectrum of the element and is denoted by . For each 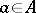the set 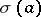is non-empty, closed and bounded.

If 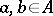, then the sets 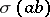and 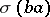need not coincide, but

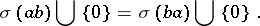The number

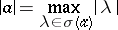is called the spectral radius of the element 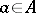; Gel'fand's formula

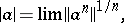where the limit on the right-hand side always exists, is valid. If 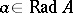, then ; the converse is true, generally speaking, only in commutative Banach algebras whose radical coincides with the set of generalized nilpotents, i.e. elements for which . In any Banach algebra the relationships 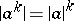, and 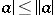are true. If 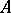is commutative, then 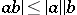and 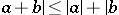are valid.

Examples of non-commutative algebras in which generalized non-zero nilpotents are absent are known. However, if 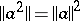for any 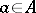, then the Banach algebra 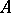is commutative. The condition 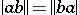for all 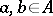is also sufficient for an algebra 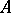with a unit to be commutative.

An algebra 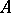is said to be an algebra with involution if an operation 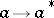is defined on 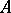that satisfies the conditions

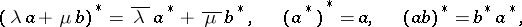for all 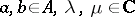. The mapping 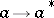is said to be an involution in 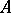. A linear functional 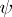on an algebra 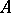with an involution is said to be positive if 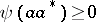for any 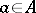. If the linear functional 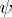is positive, then

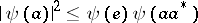for all 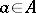. If the involution in 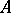is an isometry, i.e. if 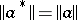for all 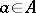, then

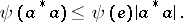A Banach algebra 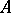with involution is said to be completely symmetric if 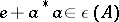for any 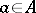; 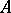is said to be a 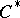-algebra (a completely-regular algebra) if for any . Any 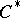-algebra is completely symmetric. Examples of completely-symmetric algebras include the group algebras 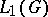of commutative or compact groups. Examples of 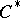-algebras include the algebras 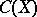(the involution in 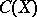is defined as transition to the complex conjugate function) and closed subalgebras of the algebra of bounded linear operators in a Hilbert space containing both the operator and the adjoint operator (involution is defined as transition to the adjoint operator). Any 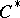-algebra is isometrically isomorphic (involution being preserved) with one of these algebras (the Gel'fand–Naimark theorem). In particular, any commutative 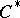-algebra 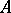is isometrically isomorphic (involution being preserved) with one of the algebras 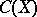(this theorem includes the Stone–Weierstrass theorem).

An element of a Banach algebra with involution is said to be Hermitian if 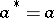. For a Banach algebra with an involution to be a 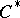-algebra it is necessary and sufficient that the condition 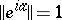be fulfilled for all Hermitian elements . If, in a Banach algebra with an involution, 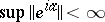(upper bound over all Hermitian elements), then this algebra is topologically -isomorphic with a 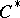-algebra. If, in an arbitrary Banach algebra, 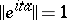for all real 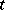for a certain fixed element , then coincides with the spectral radius, i.e. .

The theory of Banach algebras, and of commutative Banach algebras in particular, has numerous applications in various branches of functional analysis and in a number of other mathematical disciplines.

References

[1]	N. Bourbaki, "Elements of mathematics. Spectral theories" , Addison-Wesley (1977) (Translated from French)
[2]	T.W. Gamelin, "Uniform algebras" , Prentice-Hall (1969)
[3]	R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965)
[4]	I.M. Gel'fand, "Normierte Ringe" Mat. Sb. , 9 (51) : 1 (1941) pp. 3–24
[5]	A.M. Gleason, "Function algebras" , Proc. Sem. on analytic functions , 2 (1958) pp. 213–226
[6]	K. Hoffman, "Banach spaces of analytic functions" , Prentice-Hall (1962)
[7]	E.A. Gorin, "Maximal subalgebras of commutative Banach algebras with involution" Math. Notes , 1 : 2 (1967) pp. 173–178 Mat. Zametki , 1 : 2 (1967) pp. 173–178
[8]	N. Dunford, J.T. Schwartz, "Linear operators" , 1–3 , Interscience (1958–1971)
[9]	W. Zelazko, "Banach algebras" , Elsevier (1973) (Translated from Polish)
[10]	I. Kaplansky, "Functional analysis" , Surveys in applied mathematics , 4. Some aspects of analysis and probability , Wiley (1958)
[11]	L.H. Loomis, "An introduction to abstract harmonic analysis" , v. Nostrand (1953)
[12]	M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)
[13]	, Some questions in approximation theory , Moscow (1963) (In Russian; translated from English)
[14]	C.E. Rickart, "General theory of Banach algebras" , v. Nostrand (1960)
[15]	H.L. Royden, "Function algebras" Bull. Amer. Math. Soc. , 69 : 3 (1963) pp. 281–298
[16]	R.R. Phelps, "Lectures on Choquet's theorem" , v. Nostrand (1966)
[17]	E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957)

Comments

Gel'fand's formula is also called the spectral radius formula.

References

[a1]	R.V. Kadison, J.R. Ringrose, "Fundamentals of the theory of operator algebras" , 1 , Acad. Press (1983)