Unimodular group

A topological group whose left-invariant Haar measure is right invariant (equivalently, is invariant under the transformation 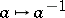). A Lie group 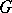is unimodular if and only if

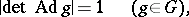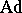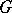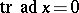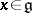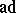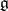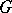where is the adjoint representation (cf. Adjoint representation of a Lie group). For a connected Lie group this is equivalent to requiring that (), where is the adjoint representation of the Lie algebra of . Any compact, discrete or Abelian locally compact group, as well as any connected reductive or nilpotent Lie group, is unimodular.

Comments

Sometimes, more rarely, the phrase unimodular group means the group of unimodular matrices (of a given size) over a ring, i.e. the group of matrices of determinant , that is more usually called the "special linear groupspecial linear group" , cf. e.g. [a3].

References

[a1]	H. Reiter, "Classical harmonic analysis and locally compact groups" , Clarendon Press (1968)
[a2]	N. Bourbaki, "Intégration" , Eléments de mathématiques , Hermann (1963) pp. Chapt. 7
[a3]	H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) pp. 45