Matrix algebra
algebra of matrices
A subalgebra of the full matrix algebra  of all
of all  -dimensional matrices over a field
-dimensional matrices over a field  . The operations in
. The operations in  are defined as follows:
are defined as follows:
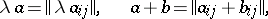 |
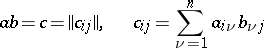 |
where  , and
, and  . The algebra
. The algebra  is isomorphic to the algebra of all endomorphisms of an
is isomorphic to the algebra of all endomorphisms of an  -dimensional vector space over
-dimensional vector space over  . The dimension of
. The dimension of  over
over  equals
equals  . Every associative algebra with an identity (cf. Associative rings and algebras) and of dimension over
. Every associative algebra with an identity (cf. Associative rings and algebras) and of dimension over 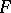 at most
at most  is isomorphic to some subalgebra of
is isomorphic to some subalgebra of  . An associative algebra without an identity and with dimension over
. An associative algebra without an identity and with dimension over  less than
less than  can also be isomorphically imbedded in
can also be isomorphically imbedded in 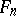 . By Wedderburn's theorem, the algebra
. By Wedderburn's theorem, the algebra 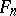 is simple, i.e. it has only trivial two-sided ideals. The centre of the algebra
is simple, i.e. it has only trivial two-sided ideals. The centre of the algebra  consists of all scalar
consists of all scalar 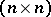 -dimensional matrices over
-dimensional matrices over  . The group of invertible elements of
. The group of invertible elements of  is the general linear group
is the general linear group 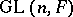 . Every automorphism
. Every automorphism  of
of  is inner:
is inner:
 |
Every irreducible matrix algebra (cf. also Irreducible matrix group) is simple. If a matrix algebra  is absolutely reducible (for example, if the field
is absolutely reducible (for example, if the field  is algebraically closed), then
is algebraically closed), then 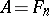 for
for 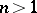 (Burnside's theorem). A matrix algebra is semi-simple if and only if it is completely reducible (cf. also Completely-reducible matrix group).
(Burnside's theorem). A matrix algebra is semi-simple if and only if it is completely reducible (cf. also Completely-reducible matrix group).
Up to conjugation, 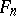 contains a unique maximal nilpotent subalgebra — the algebra of all upper-triangular matrices with zero diagonal entries. In
contains a unique maximal nilpotent subalgebra — the algebra of all upper-triangular matrices with zero diagonal entries. In 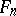 there is an
there is an  -dimensional commutative subalgebra if and only if
-dimensional commutative subalgebra if and only if
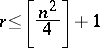 |
(Schur's theorem). Over the complex field 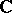 the set of conjugacy classes of maximal commutative subalgebras of
the set of conjugacy classes of maximal commutative subalgebras of  is finite for
is finite for 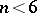 and infinite for
and infinite for 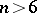 .
.
In 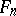 one has the standard identity of degree
one has the standard identity of degree 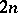 :
:
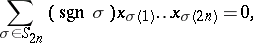 |
where 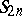 denotes the symmetric group and
denotes the symmetric group and  the sign of the permutation
the sign of the permutation 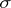 , but no identity of lower degree.
, but no identity of lower degree.
References
| [1] | H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) |
| [2] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
| [3] | I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968) |
| [4] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [5] | D.A. Suprunenko, R.I. Tyshkevich, "Commutable matrices" , Minsk (1966) (In Russian) |
Comments
A frequently used notation for  is
is 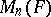 .
.
Wedderburn's theorem on the structure of semi-simple rings says that any semi-simple ring 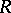 is a finite direct product of full matrix rings
is a finite direct product of full matrix rings 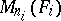 over skew-fields
over skew-fields  , and conversely every ring of this form is semi-simple. Further, the
, and conversely every ring of this form is semi-simple. Further, the  and
and 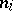 are uniquely determined by
are uniquely determined by 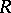 .
.
The Wedderburn–Artin theorem says that a right Artinian simple ring is a total matrix ring (E. Artin, 1928; proved for finite-dimensional algebras by J.H.M. Wedderburn in 1907). A far-reaching generalization of this is the Jacobson density theorem, cf. Associative rings and algebras and [a1].
References
| [a1] | P.M. Cohn, "Algebra" , 2 , Wiley (1977) pp. Sect. 10.2 |
Matrix algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_algebra&oldid=24161