Voronoi diagram
From Encyclopedia of Mathematics
A very important geometric structure in computational geometry, named after G.F. Voronoi. The earliest significant use of Voronoi diagrams seems to have occurred in the work of C.F. Gauss, P.G.L. Dirichlet and Voronoi on the reducibility of positive-definite quadratic forms (cf. Quadratic form).
Let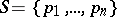 
be a set of 
points in 
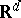. The Voronoi diagram generated by 
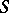is the partition of the 
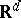into 
convex cells, the Voronoi cells,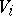 
, where each 
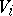contains all points of 
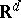closer to 
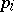than to any other point:
 |
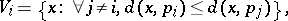where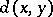 
is the Euclidean distance between 
and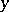 
.
See also Delaunay triangulation.
References
| [a1] | F.P. Preparata, M.I. Shamos, "Computational geometry: an introduction" , Springer (1985) |
| [a2] | H. Edelsbrunner, "Algorithms in combinatorial geometry" , Springer (1987) |
| [a3] | A. Okabe, B. Boots, K. Sugihara, "Spatial tessellations: concepts and applications of Voronoi diagrams" , Wiley (1992) |
| [a4] | G.F. Voronoi, "Nouvelles applications des parametres continus a la theorie des formes quadratiques" J. Reine Angew. Math. , 134 (1908) pp. 198–287 |
How to Cite This Entry:
Voronoi diagram. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Voronoi_diagram&oldid=24136
Voronoi diagram. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Voronoi_diagram&oldid=24136
This article was adapted from an original article by O.R. Musin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article