Bott periodicity theorem

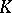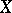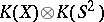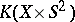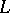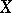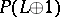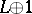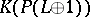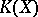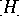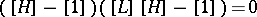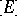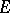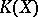A fundamental theorem in -theory which, in its simplest form, states that for any (compact) space there exists an isomorphism between the rings and . More generally, if is a complex vector bundle over and is the projectivization of , then the ring is a -algebra with one generator and a unique relation , where is the image of a vector bundle in and 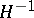is the Hopf fibration over 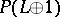. This fact is equivalent to the existence of a Thom isomorphism in 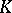-theory for complex vector bundles. In particular, 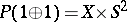. Bott's periodicity theorem was first demonstrated by R. Bott [1] using Morse theory, and was then re-formulated in terms of 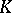-theory [6]; an analogous theorem has also been demonstrated for real fibre bundles.

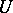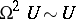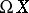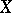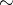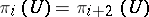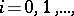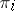Bott's periodicity theorem establishes the property of the stable homotopy type of the unitary group , consisting in the fact that , where is the space of loops on , and is weak homotopy equivalence, in particular for where is the 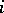-th homotopy group. Similarly, for the orthogonal group :

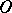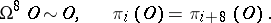References

[1]	R. Bott, "The stable homotopy of the classical groups" Ann. of Math. (2) , 70 : 2 (1959) pp. 313–337
[2]	J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963)
[3]	M.F. Atiyah, "-theory: lectures" , Benjamin (1967)
[4]	D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)
[5]	J.C. Moore, "On the periodicity theorem for complex vector bundles" , Sem. H. Cartan (1959–1960)
[6]	M.F. Atiyah, R. Bott, "On the periodicity theorem for complex vector bundles" Acta Math. , 112 (1964) pp. 229–247

References

[a1]	R. Bott, "Lectures on " , Benjamin (1969)
[a2]	M. Karoubi, "-theory" , Springer (1978)