Torelli theorems
Theorems stating that the Hodge structure (period matrix) in the cohomology spaces  of an algebraic or Kähler variety
of an algebraic or Kähler variety 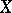 completely characterizes the polarized Jacobi variety of
completely characterizes the polarized Jacobi variety of 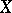 .
.
The classical Torelli theorem relates to the case of curves (see [1], [2]) and states that a curve is defined up to an isomorphism by its periods. Let 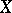 be a curve of genus
be a curve of genus 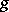 , let
, let 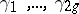 be a basis of
be a basis of 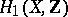 , let
, let 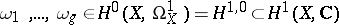 be a basis of the Abelian differentials (cf. Abelian differential) and let the
be a basis of the Abelian differentials (cf. Abelian differential) and let the 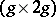 -matrix
-matrix 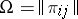 be the period matrix, where
be the period matrix, where 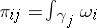 . The intersection of cycles
. The intersection of cycles 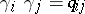 defines a skew-symmetric bilinear form
defines a skew-symmetric bilinear form 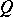 in
in 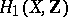 . Let
. Let 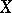 and
and 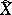 be two curves. If bases
be two curves. If bases  and
and 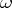 can be chosen with respect to which the period matrices
can be chosen with respect to which the period matrices  and the intersection matrices
and the intersection matrices 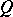 of the curves are the same, then
of the curves are the same, then 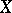 and
and 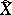 are isomorphic. In other words, if the canonically polarized Jacobians of the curves
are isomorphic. In other words, if the canonically polarized Jacobians of the curves 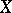 and
and 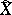 are isomorphic, then
are isomorphic, then 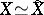 .
.
Let 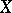 be a projective variety (or, more generally, a compact Kähler manifold), and let
be a projective variety (or, more generally, a compact Kähler manifold), and let  be the Griffiths variety associated with the primitive cohomology spaces
be the Griffiths variety associated with the primitive cohomology spaces 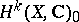 (see Period mapping). Then
(see Period mapping). Then 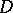 contains the period matrices of primitive
contains the period matrices of primitive 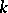 -forms on all varieties homeomorphic to
-forms on all varieties homeomorphic to 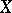 . The periods depend on the choice of the isomorphism of
. The periods depend on the choice of the isomorphism of 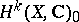 into a fixed space
into a fixed space 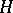 . There is a naturally defined group
. There is a naturally defined group 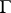 of analytic automorphisms of
of analytic automorphisms of 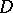 such that
such that 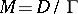 is an analytic space and
is an analytic space and 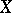 determines a unique point
determines a unique point  . In this situation,
. In this situation, 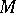 is called the modular space or the moduli space of Hodge structures.
is called the modular space or the moduli space of Hodge structures.
The global Torelli problem consists in the elucidation of the question whether 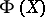 uniquely determines
uniquely determines 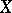 up to an isomorphism. In the case of an affirmative solution, the problem corresponds to the statement of the so-called (generalized) Torelli theorem. Torelli's theorem holds trivially for Abelian varieties in the case of
up to an isomorphism. In the case of an affirmative solution, the problem corresponds to the statement of the so-called (generalized) Torelli theorem. Torelli's theorem holds trivially for Abelian varieties in the case of 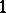 -forms and in the case of
-forms and in the case of  -forms (see [3]). Essentially, the only non-trivial case of a solution of the global Torelli problem (1984) is the case of a
-forms (see [3]). Essentially, the only non-trivial case of a solution of the global Torelli problem (1984) is the case of a 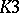 -surface. The Torelli theorem has also been generalized to the case of Kähler
-surface. The Torelli theorem has also been generalized to the case of Kähler 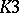 -surfaces.
-surfaces.
The local Torelli problem consists in solving the question when the Hodge structures on the cohomology spaces separate points in the local moduli space (the Kuranishi space) for a variety 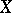 . Let
. Let 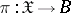 be a family of polarized algebraic varieties,
be a family of polarized algebraic varieties, 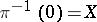 , and let
, and let 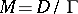 be the Griffiths variety associated with the periods of primitive
be the Griffiths variety associated with the periods of primitive 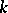 -forms on
-forms on 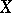 . The period mapping
. The period mapping 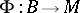 associates
associates 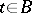 with the period matrix of
with the period matrix of 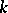 -forms on
-forms on 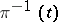 . This mapping is holomorphic; the corresponding tangent mapping
. This mapping is holomorphic; the corresponding tangent mapping 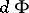 has been calculated (see [3]). The local Torelli problem is equivalent to the question: When is
has been calculated (see [3]). The local Torelli problem is equivalent to the question: When is 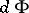 an imbedding? By considering the mapping dual to
an imbedding? By considering the mapping dual to 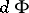 one obtains a cohomological criterion for the validity of the local Torelli theorem: If the mapping
one obtains a cohomological criterion for the validity of the local Torelli theorem: If the mapping
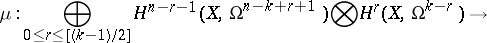 |
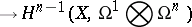 |
is an epimorphism, then the periods of the 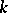 -forms give local moduli for
-forms give local moduli for 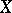 . The local Torelli theorem for curves is equivalent to the fact that quadratic differentials are generated by Abelian differentials. Noether's theorem states that this is true if
. The local Torelli theorem for curves is equivalent to the fact that quadratic differentials are generated by Abelian differentials. Noether's theorem states that this is true if 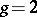 or if
or if 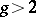 and
and 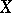 is not hyper-elliptic. The local Torelli theorem clearly holds in the case
is not hyper-elliptic. The local Torelli theorem clearly holds in the case 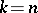 if the canonical class is trivial. Such varieties include the Abelian varieties, hypersurfaces of degree
if the canonical class is trivial. Such varieties include the Abelian varieties, hypersurfaces of degree 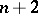 in
in 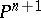 and
and 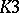 -surfaces. The validity of the local Torelli theorem has been established for various classes of higher-dimensional varieties. For non-singular hypersurfaces of degree
-surfaces. The validity of the local Torelli theorem has been established for various classes of higher-dimensional varieties. For non-singular hypersurfaces of degree 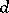 in
in 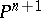 it has been proved that the period mapping is an imbedding at a generic point except for the case
it has been proved that the period mapping is an imbedding at a generic point except for the case 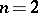 ,
, 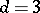 and, possibly, the cases:
and, possibly, the cases: 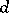 divides
divides 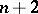 ,
, 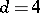 and
and 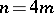 , or
, or 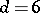 and
and 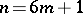 (see [4]).
(see [4]).
References
| [1] | R. Torelli, Rend. Accad. Lincei V , 22 (1913) pp. 98–103 |
| [2] | A. Weil, "Zum Beweis der Torellischen Satzes" Nachr. Akad. Wiss. Göttingen (1957) pp. 33–53 |
| [3] | P.A. Griffiths, "Periods of integrals on algebraic manifolds I, II" Amer. J. Math. , 90 (1968) pp. 568–626; 805–865 |
| [4] | R. Donagi, "Generic Torelli for projective hypersurfaces" Compos. Math. , 50 (1983) pp. 325–353 |
Comments
References
| [a1] | P.A. Griffiths (ed.) , Topics in transcendental algebraic geometry , Princeton Univ. Press (1984) |
| [a2] | A. van de Ven, "Compact complex surfaces" , Springer (1984) |
Torelli theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Torelli_theorems&oldid=23999