Tate conjectures
Conjectures expressed by J. Tate (see [1]) and describing relations between Diophantine and algebro-geometric properties of an algebraic variety.
Conjecture 1. If the field 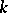 is finitely generated over its prime subfield, if
is finitely generated over its prime subfield, if 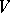 is a smooth projective variety over
is a smooth projective variety over 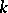 , if
, if 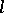 is a prime number different from the characteristic of the field
is a prime number different from the characteristic of the field 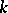 , if
, if
 |
is the natural 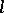 -adic representation, and
-adic representation, and 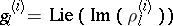 , then the
, then the  -space
-space 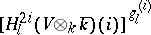 , the space of elements of
, the space of elements of 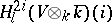 annihilated by
annihilated by 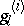 , is generated by the homology classes of algebraic cycles of codimension
, is generated by the homology classes of algebraic cycles of codimension 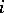 on
on 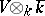 (cf. also Algebraic cycle).
(cf. also Algebraic cycle).
Conjecture 2. The rank of the group of classes of algebraic cycles of codimension 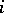 on
on 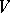 modulo homology equivalence coincides with the order of the pole of the function
modulo homology equivalence coincides with the order of the pole of the function 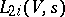 at the point
at the point 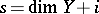 .
.
These conjectures were verified for a large number of particular cases; restrictions are imposed both on the field 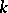 and on the variety
and on the variety 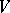 .
.
References
| [1] | J.T. Tate, "Algebraic cycles and poles of zeta-functions" D.F.G. Schilling (ed.) , Arithmetical Algebraic geometry (Proc. Purdue Conf. 1963) , Harper & Row (1965) pp. 93–110 |
Comments
In conjecture 2 above 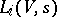 is the
is the 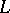 -series of
-series of  , defined by
, defined by
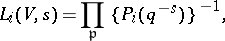 |
where the product is over all primes 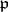 where
where 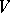 has good reduction and where
has good reduction and where 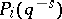 is the
is the 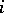 -th polynomial factor appearing in the zeta-function of the variety
-th polynomial factor appearing in the zeta-function of the variety 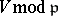 over the residue field
over the residue field 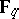 of
of 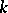 at
at 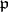 ,
,
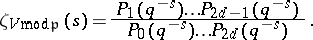 |
In the case 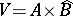 , with
, with 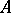 and
and  Abelian varieties, conjecture 1 takes for
Abelian varieties, conjecture 1 takes for  (i.e. for divisors) the following form: The natural homomorphism
(i.e. for divisors) the following form: The natural homomorphism
 |
is an isomorphism (where 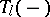 is the Tate module of the Abelian variety) (see [1]). This case of the conjecture has been proved: i)
is the Tate module of the Abelian variety) (see [1]). This case of the conjecture has been proved: i)  is a finite field by J. Tate [a1]; ii) if
is a finite field by J. Tate [a1]; ii) if 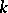 is a function field over a finite field by J.G. Zarkin [a2]; and iii) if
is a function field over a finite field by J.G. Zarkin [a2]; and iii) if 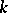 is a number field by G. Faltings [a3].
is a number field by G. Faltings [a3].
For examples of particular cases where the Tate conjecture has been proved see, e.g., [a4] for ordinary 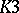 -surfaces over finite fields and [a5] for Hilbert modular surfaces.
-surfaces over finite fields and [a5] for Hilbert modular surfaces.
References
| [a1] | J. Tate, "Endomorphisms of Abelian varieties over finite fields" Invent. Math. , 2 (1966) pp. 104–145 |
| [a2] | J.G. Zarking, "A remark on endomorphisms of Abelian varieties over function fields of finite characteristic" Math. USSR Izv. , 8 (1974) pp. 477–480 Izv. Akad. Nauk SSSR , 38 : 3 (1974) pp. 471–474 |
| [a3] | G. Faltings, "Endlichkeitssätze für abelsche Varietäten über Zahlkörpern" Invent. Math. , 73 (1983) pp. 349–366 (Erratum: Invent. Math 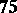 (1984), 381) (1984), 381) |
| [a4] | N.O. Nygaard, "The Tate conjecture for ordinary 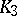 -surfaces over finite fields" Invent. Math. , 74 (1983) pp. 213–237 -surfaces over finite fields" Invent. Math. , 74 (1983) pp. 213–237 |
| [a5] | G. van der Geer, "Hilbert modular surfaces" , Springer (1987) |
| [a6] | G. Wüstholz (ed.) , Rational points , Vieweg (1984) |
Tate conjectures. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tate_conjectures&oldid=23992