Segre imbedding
From Encyclopedia of Mathematics
The imbedding 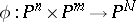 of the product
of the product 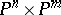 of projective spaces into the projective space
of projective spaces into the projective space  , where
, where 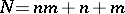 . If
. If 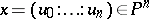 ,
, 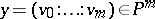 , and
, and 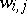 (
(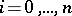 ;
;  ) are homogeneous coordinates in
) are homogeneous coordinates in 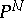 , then the mapping is defined by the formula:
, then the mapping is defined by the formula:
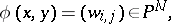 |
where  . The mapping
. The mapping 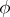 is well-defined and is a closed imbedding. The image
is well-defined and is a closed imbedding. The image 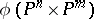 of a Segre imbedding is called a Segre variety. The case when
of a Segre imbedding is called a Segre variety. The case when  has a simple geometrical meaning:
has a simple geometrical meaning: 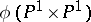 is the non-singular quadric in
is the non-singular quadric in 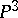 with equation
with equation 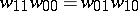 . The images
. The images 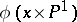 and
and 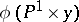 give two families of generating lines of the quadric.
give two families of generating lines of the quadric.
The terminology is in honour of B. Segre.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 |
How to Cite This Entry:
Segre imbedding. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Segre_imbedding&oldid=23973
Segre imbedding. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Segre_imbedding&oldid=23973
This article was adapted from an original article by Val.S. Kulikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article