Point in general position

A point on an algebraic variety that belongs to an open and dense subset in the Zariski topology. In algebraic geometry a point in general position is often called simply a generic point.

Comments

More precisely, a point is said to be in general position if it is outside a certain (given, or to be described) closed set; a point in an irreducible set 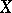is called generic if it is outside every closed set different from 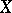itself.

In differential topology, the phrase "a point in general position" often is used in the sense of a generic point, which is roughly "a point with no particular relationship of current importance to other structure elements being considered" . The precise meaning depends on the context. An element generically has a certain property if the property holds outside (a countable intersection of) open dense set(s). For instance, a polynomial has generically no double roots. Two submanifolds are in general position if they "intersect as little as possible" . If 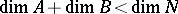, this means ; if 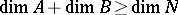, then for every 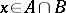, 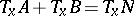. Any non-general position situation can be changed to a general position situation by an arbitrarily small change, while if things are in general position, then sufficiently small changes do not change that. A precise version of general position is transversality, cf. also Transversality condition.

References

[a1]	R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91
[a2]	M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78
[a3]	D.R.J. Chillingworth, "Differential topology with a view to applications" , Pitman (1976) pp. 221ff