Ordered ring

partially ordered ring

A ring (not necessarily associative) which is a partially ordered group under addition and in which for any elements the inequalities and imply and . Every ring is an ordered ring for the trivial order. As examples of ordered rings one may take an ordered field; the ring of real functions on a set , where means that for all 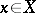; or a matrix ring over an ordered ring 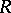, where, by definition, if 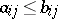for all 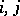. If 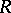is an ordered ring, then the set

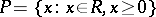is called its positive cone. The positive cone of an ordered ring completely defines the order: 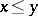if and only if 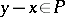. A subset 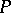of a ring 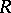can serve as the positive cone for some order if and only if

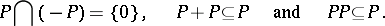The equation 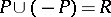is equivalent to the totality of the order (cf. Totally ordered set).

An ordered ring that is totally ordered or lattice-ordered is accordingly called a totally ordered or lattice-ordered ring (cf. also Archimedean ring). Lattice-ordered rings turn out to be distributive lattices, and their additive groups are torsion-free (cf. Lattice-ordered group). Certain questions in the theory of associative rings and, in particular, in the theory of radicals have analogues in associative lattice-ordered rings. The class of rings which allow a lattice-ordered ring structure is not axiomatizable. If 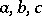are elements of a lattice-ordered ring and 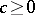, then the following relations hold:

Ideals in lattice-ordered rings which are convex subgroups (cf. Convex subgroup) of the additive group are called -ideals. The quotient ring by an 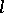-ideal can be made into a lattice-ordered ring in a natural way. The homomorphism theorem holds.

A lattice-ordered ring 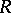is called a functional ring or an 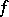-ring if it satisfies any of the following equivalent conditions: 1) 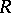is isomorphic to a lattice-ordered subring of a direct product of totally ordered rings; 2) for any one has the implication

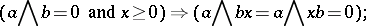3) for any subset 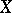of the set

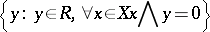is an 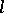-ideal; and 4) for any ,

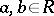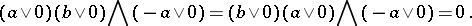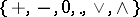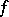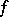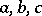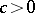Condition 4) shows that -rings form a variety of signature . Neither of the equations in this condition is a consequence of the other. Not every -ring can be imbedded in an -ring with a unit element. If are elements of an -ring and , then one has

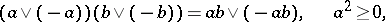as well as the implication .

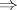
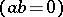An order of an ordered ring 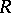with a positive cone 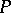can be extended to a total order such that 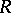becomes a totally ordered ring if and only if for any finite set in 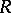one can choose or such that in the semi-ring generated by 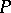and the elements the sum of any two non-zero elements is non-zero. With 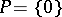one obtains a criterion for the possibility of having a total order on the ring.

References

[1]	G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973)
[2]	A.A. Vinogradov, "The non-axiomatizability of lattice-ordered rings" Math. Notes , 21 (1977) pp. 253–254 Mat. Zametki , 21 : 4 (1977) pp. 449–452
[3]	L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963)
[4]	A. Bigard, K. Keimel, S. Wolfenstein, "Groupes et anneaux reticulés" , Springer (1977)
[5]	G.W. Brumfiel, "Partially ordered rings and semi-algebraic geometry" , Cambridge Univ. Press (1979)
[6]	S.A. Steinberg, "Radical theory in lattice-ordered rings" Symp. Mat. Ist. Naz. Alta Mat. , 21 (1977) pp. 379–400
[7]	S.A. Steinberg, "Examples of lattice-ordered rings" J. of Algebra , 72 : 1 (1981) pp. 223–236

Comments

For a survey of the current state-of-the-art in the field see the second part of [a1].

References

[a1]	J. Martinez (ed.) , Ordered algebraic structures , Kluwer (1989)