Artin approximation
Let 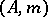 be a Noetherian local ring and
be a Noetherian local ring and 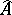 its completion.
its completion. 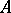 has the Artin approximation property (in brief,
has the Artin approximation property (in brief, 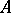 has AP) if every finite system of polynomial equations over
has AP) if every finite system of polynomial equations over 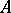 has a solution in
has a solution in 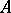 if it has one in
if it has one in 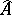 . In fact,
. In fact, 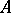 has the Artin approximation property if and only if for every finite system of polynomial equations
has the Artin approximation property if and only if for every finite system of polynomial equations 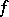 over
over 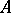 the set of its solutions in
the set of its solutions in 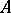 is dense, with respect to the
is dense, with respect to the 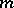 -adic topology, in the set of its solutions in
-adic topology, in the set of its solutions in 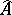 . That is, for every solution
. That is, for every solution 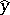 of
of 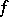 in
in  and every positive integer
and every positive integer 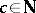 there exists a solution
there exists a solution 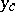 of
of 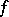 in
in 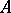 such that
such that 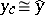 modulo
modulo 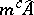 . The study of Artin approximation started with the famous papers of M. Artin [a3], [a4], which state that the convergent power series rings over a non-trivial valued field of characteristic zero, the Henselization of a local ring essentially of finite type over a field, and an excellent Dedekind ring all have the Artin approximation property. The first result was extended by M. André [a1] to certain convergent formal power series rings over a field of non-zero characteristic.
. The study of Artin approximation started with the famous papers of M. Artin [a3], [a4], which state that the convergent power series rings over a non-trivial valued field of characteristic zero, the Henselization of a local ring essentially of finite type over a field, and an excellent Dedekind ring all have the Artin approximation property. The first result was extended by M. André [a1] to certain convergent formal power series rings over a field of non-zero characteristic.
The following assertion holds: A Noetherian local ring has AP if and only if it is excellent and Henselian.
The necessity is stated in [a24], a weaker result, namely that AP implies Henselian and universally Japanese, being proved in [a14], (5.4), and [a9]. The sufficiency gives a positive answer to Artin's conjecture [a5] and is a consequence (see [a21], (1.3), and [a27]) of the following theorem on general Néron desingularization ([a20], [a21], [a23], [a2], [a16], [a27], [a26]): A morphism 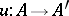 between Noetherian rings is regular (i.e. it is flat and for every field
between Noetherian rings is regular (i.e. it is flat and for every field 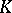 that is a finite
that is a finite 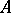 -algebra, the ring
-algebra, the ring 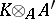 is regular) if and only if it is a filtered inductive limit of smooth algebras of finite type.
is regular) if and only if it is a filtered inductive limit of smooth algebras of finite type.
Roughly speaking, general Néron desingularization says in particular that if  is a regular morphism of Noetherian rings, then every finite system of polynomial equations over
is a regular morphism of Noetherian rings, then every finite system of polynomial equations over 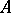 having a solution in
having a solution in 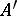 can be enlarged to a finite system of polynomial equations over
can be enlarged to a finite system of polynomial equations over 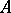 having a solution in
having a solution in  , for which one may apply the implicit function theorem. Another consequence of general Néron desingularization says that a regular local ring containing a field is a filtered inductive limit of regular local rings essentially of finite type over
, for which one may apply the implicit function theorem. Another consequence of general Néron desingularization says that a regular local ring containing a field is a filtered inductive limit of regular local rings essentially of finite type over 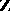 . This is a partial positive answer to the Swan conjecture and, using [a15], proves the Bass–Quillen conjecture in the equicharacteristic case (see also [a22], [a27]).
. This is a partial positive answer to the Swan conjecture and, using [a15], proves the Bass–Quillen conjecture in the equicharacteristic case (see also [a22], [a27]).
Let 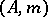 be a Noetherian local ring.
be a Noetherian local ring. 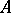 has the strong Artin approximation property (in brief,
has the strong Artin approximation property (in brief, 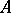 has SAP) if for every finite system of equations
has SAP) if for every finite system of equations  in
in 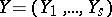 over
over 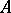 there exists a mapping
there exists a mapping 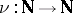 with the following property: If
with the following property: If 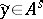 satisfies
satisfies 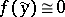 modulo
modulo 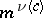 ,
, 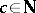 , then there exists a solution
, then there exists a solution 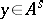 of
of 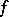 with
with 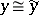 modulo
modulo 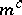 .
.
M. Greenberg [a13] proved that excellent Henselian discrete valuation rings have the strong Artin approximation property and M. Artin [a4] showed that the Henselization of a local ring which is essentially of finite type over a field has the strong Artin approximation property.
The following assertion is true: A Noetherian complete local ring 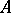 has the strong Artin approximation property. In particular,
has the strong Artin approximation property. In particular, 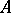 has AP if and only if it has SAP. A special case of this is stated in [a11], together with many other applications.
has AP if and only if it has SAP. A special case of this is stated in [a11], together with many other applications.
When 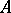 contains a field, some weaker results were stated in [a29], [a30]. In the above form, the result appeared in [a17], but the proof there has a gap in the non-separable case, which was repaired in [a14], Chap. 2. In [a8] it was noted that SAP is more easily handled using ultraproducts. Let
contains a field, some weaker results were stated in [a29], [a30]. In the above form, the result appeared in [a17], but the proof there has a gap in the non-separable case, which was repaired in [a14], Chap. 2. In [a8] it was noted that SAP is more easily handled using ultraproducts. Let 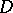 be a non-principal ultrafilter on
be a non-principal ultrafilter on 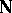 (i.e. an ultrafilter containing the filter of cofinite sets of
(i.e. an ultrafilter containing the filter of cofinite sets of 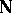 ). The ultraproduct
). The ultraproduct 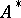 of
of 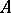 with respect to
with respect to 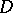 is the factor of
is the factor of 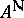 by the ideal of all
by the ideal of all 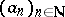 such that the set
such that the set 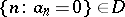 . Assigning to
. Assigning to 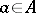 the constant sequence
the constant sequence 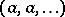 one obtains a ring morphism
one obtains a ring morphism 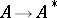 . Using these concepts, easier proofs of the assertion were given in [a19] and [a10]. The easiest one is given in [a21], (4.5), where it is noted that the separation
. Using these concepts, easier proofs of the assertion were given in [a19] and [a10]. The easiest one is given in [a21], (4.5), where it is noted that the separation 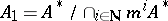 of
of 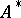 in the
in the 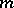 -adic topology is Noetherian, that the canonical mapping
-adic topology is Noetherian, that the canonical mapping 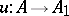 is regular if
is regular if 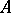 is excellent and that
is excellent and that 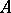 is SAP if and only if for every finite system of polynomial equations
is SAP if and only if for every finite system of polynomial equations 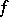 over
over 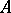 , for every positive integer
, for every positive integer  and every solution
and every solution 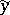 of
of 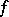 in
in  , there exists a solution
, there exists a solution 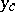 of
of 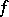 in
in 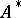 which lifts
which lifts 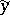 modulo
modulo  . The result follows on applying general Néron desingularization to
. The result follows on applying general Néron desingularization to  and using the implicit function theorem.
and using the implicit function theorem.
Theorems on Artin approximation have many direct applications in algebraic geometry (for example, to the algebraization of versal deformations and the construction of algebraic spaces; see [a6], [a5]), in algebraic number theory and in commutative algebra (see [a4], [a14], Chaps. 5, 6). For example, if  is a Noetherian complete local domain and
is a Noetherian complete local domain and 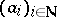 is a sequence of elements from
is a sequence of elements from 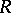 converging to an irreducible element
converging to an irreducible element  of
of 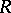 , then G. Pfister proved that
, then G. Pfister proved that 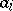 is irreducible for
is irreducible for  (see [a14], Chap. 5). Using these ideas, a study of approximation of prime ideals in the
(see [a14], Chap. 5). Using these ideas, a study of approximation of prime ideals in the 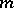 -adic topology was given in [a18]. Another application is that the completion of an excellent Henselian local domain
-adic topology was given in [a18]. Another application is that the completion of an excellent Henselian local domain 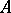 is factorial if and only if
is factorial if and only if 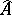 is factorial [a21], (3.4).
is factorial [a21], (3.4).
All these approximation properties were studied also for couples  , were
, were 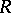 is not necessarily local and
is not necessarily local and  is not necessarily maximal. A similar proof shows that the Artin approximation property holds for a Henselian couple
is not necessarily maximal. A similar proof shows that the Artin approximation property holds for a Henselian couple 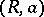 if
if 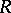 is excellent [a21], (1.3). If
is excellent [a21], (1.3). If 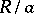 is not Artinian, then
is not Artinian, then 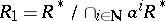 is not Noetherian and SAP cannot hold in this setting, because one cannot apply general Néron desingularization. Moreover, the SAP property does not hold for general couples, as noticed in [a25].
is not Noetherian and SAP cannot hold in this setting, because one cannot apply general Néron desingularization. Moreover, the SAP property does not hold for general couples, as noticed in [a25].
A special type of Artin approximation theory was required in singularity theory. Such types were studied in [a14], Chaps. 3, 4. However, the result holds even in the following extended form: Let 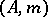 be an excellent Henselian local ring,
be an excellent Henselian local ring, 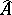 its completion,
its completion, 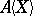 the Henselization of
the Henselization of 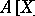 ,
, 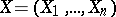 , in
, in 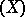 ,
, 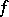 a finite system of polynomial equations over
a finite system of polynomial equations over 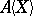 and
and 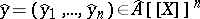 a formal solution of
a formal solution of 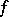 such that
such that 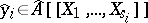 ,
, 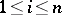 , for some positive integers
, for some positive integers 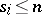 . Then there exists a solution
. Then there exists a solution 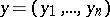 of
of 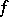 in
in 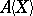 such that
such that 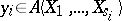 ,
, 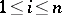 , and
, and 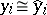 modulo
modulo 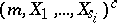 ,
, 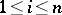 , for
, for 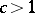 .
.
The proof is given in [a21], (3.6), (3.7), using ideas of H. Kurke and Pfister, who noticed that this assertion holds if 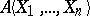 has AP, where
has AP, where 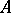 is an excellent Henselian local ring. If the sets of variables
is an excellent Henselian local ring. If the sets of variables 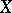 of
of 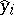 are not "nested" (i.e. they are not totally ordered by inclusion), then the assertion does not hold, see [a7]. If
are not "nested" (i.e. they are not totally ordered by inclusion), then the assertion does not hold, see [a7]. If 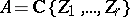 is the convergent power series ring over
is the convergent power series ring over  and the algebraic power series rings
and the algebraic power series rings 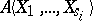 are replaced by
are replaced by 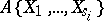 , then the theorem does not hold, see [a12]. Extensions of this theorem are given in [a28], [a27].
, then the theorem does not hold, see [a12]. Extensions of this theorem are given in [a28], [a27].
References
| [a1] | M. André, "Artin's theorem on the solution of analytic equations in positive characteristic" Manuscripta Math. , 15 (1975) pp. 314–348 |
| [a2] | M. André, "Cinq exposés sur la desingularization" École Polytechn. Féd. Lausanne (1991) (Handwritten manuscript) |
| [a3] | M. Artin, "On the solution of analytic equations" Invent. Math. , 5 (1968) pp. 277–291 |
| [a4] | M. Artin, "Algebraic approximation of structures over complete local rings" Publ. Math. IHES , 36 (1969) pp. 23–58 |
| [a5] | M. Artin, "Construction techniques for algebraic spaces" , Actes Congres Internat. Math. , 1 (1970) pp. 419–423 |
| [a6] | M. Artin, "Versal Deformations and Algebraic Stacks" Invent. Math. , 27 (1974) pp. 165–189 |
| [a7] | J. Becker, "A counterexample to Artin approximation with respect to subrings" Math. Ann. , 230 (1977) pp. 195–196 |
| [a8] | J. Becker, J. Denef, L. Lipshitz, L. van den Dries, "Ultraproducts and approximation in local rings I" Invent. Math. , 51 (1979) pp. 189–203 |
| [a9] | M. Cipu, D. Popescu, "Some extensions of Néron's  -desingularization and approximation" Rev. Roum. Math. Pures Appl. , 24 : 10 (1981) pp. 1299–1304 -desingularization and approximation" Rev. Roum. Math. Pures Appl. , 24 : 10 (1981) pp. 1299–1304 |
| [a10] | J. Denef, L. Lipshitz, "Ultraproducts and approximation in local rings II" Math. Ann. , 253 (1980) pp. 1–28 |
| [a11] | R. Elkik, "Solutions d'equations à coefficients dans une anneau (!!) henselien" Ann. Sci. Ecole Norm. Sup. 4 , 6 (1973) pp. 533–604 |
| [a12] | A.M. Gabrielov, "The formal relations between analytic functions" Funkts. Anal. Prilozh. , 5 : 4 (1971) pp. 64–65 (In Russian) |
| [a13] | M. Greenberg, "Rational points in Henselian discrete valuation rings" Publ. Math. IHES , 31 (1966) pp. 59–64 |
| [a14] | H. Kurke, T. Mostowski, G. Pfister, D. Popescu, M. Roczen, "Die Approximationseigenschaft lokaler Ringe" , Lecture Notes Math. , 634 , Springer (1978) (Note: The proof of (3.1.1) is wrong) |
| [a15] | H. Lindel, "On the Bass–Quillen conjecture concerning projective modules over polynomial rings" Invent. Math. , 65 (1981) pp. 319–323 |
| [a16] | T. Ogoma, "General Néron desingularization based on the idea of Popescu" J. Algebra , 167 (1994) pp. 57–84 |
| [a17] | G. Pfister, D. Popescu, "Die strenge Approximationseigenschaft lokaler Ringe" Invent. Math. , 30 (1975) pp. 145–174 |
| [a18] | G. Pfister, D. Popescu, "Die Approximation von Primidealen" Bull. Acad. Polon. Sci. , 27 (1979) pp. 771–778 |
| [a19] | D. Popescu, "Algebraically pure morphisms" Rev. Roum. Math. Pures Appl. , 26 : 6 (1979) pp. 947–977 |
| [a20] | D. Popescu, "General Néron desingularization" Nagoya Math. J. , 100 (1985) pp. 97–126 |
| [a21] | D. Popescu, "General Néron desingularization and approximation" Nagoya Math. J. , 104 (1986) pp. 85–115 |
| [a22] | D. Popescu, "Polynomial rings and their projective modules" Nagoya Math. J. , 113 (1989) pp. 121–128 |
| [a23] | D. Popescu, "Letter to the Editor: General Néron desingularization and approximation" Nagoya Math. J. , 118 (1990) pp. 45–53 |
| [a24] | C. Rotthaus, "Rings with approximation property" Math. Ann. , 287 (1990) pp. 455–466 |
| [a25] | M. Spivakovsky, "Non-existence of the Artin function for Henselian pairs" Math. Ann. , 299 (1994) pp. 727–729 |
| [a26] | M. Spivakovsky, "A new proof of D. Popescu's theorem on smoothing of ring homomorphisms" J. Amer. Math. Soc. , 294 (to appear) |
| [a27] | R. Swan, "Néron–Popescu desingularization" , Proc. Internat. Conf. Algebra and Geometry, Taipei, Taiwan, 1995 , Internat. Press Boston (1998) |
| [a28] | B. Teissier, "Résultats récents sur l'approximation des morphisms en algèbre commutative,[d'après Artin, Popescu, André, Spivakovsky]" Sem. Bourbaki , 784 (1994) pp. 1–15 |
| [a29] | M. Van der Put, "A problem on coefficient fields and equations over local rings" Compositio Math. , 30 : 3 (1975) pp. 235–258 |
| [a30] | J.J. Wavrik, "A theorem on solutions of analytic equations with applications to deformations of complex structures" Math. Ann. , 216 : 2 (1975) pp. 127–142 |
Artin approximation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Artin_approximation&oldid=23758