Plücker interpretation

A model that realizes the geometry of the three-dimensional projective space 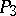in the hyperbolic space 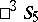. The Plücker interpretation is based on a special interpretation of the Plücker coordinates of a straight line, which are defined for any straight line in .

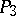Under projective transformations of 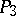the Plücker coordinates transform linearly; the Plücker coordinates of straight lines in 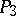give a one-to-one correspondence between the straight lines of 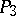and the points in the projective space 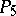whose coordinates are numerically equal to the Plücker coordinates in .

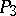Straight lines in 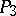are represented by the points of a non-singular quadric in 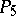of index three.

If one takes this quadric as the absolute and defines a projective (non-Euclidean) metric in 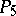, one gets the five-dimensional hyperbolic space 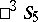. Under each collineation and correlation of 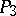the Plücker coordinates transform linearly, i.e. each collineation and correlation is represented by a collineation of 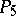that maps the absolute into itself. These collineations are thus displacements of 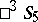. The displacements of 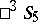represent either collineations or correlations in .

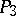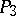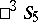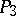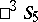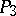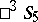Each line complex in is put into correspondence with a point in . The projective geometry of can be considered as a non-Euclidean geometry of . This interpretation of the geometry of in is called the Plücker interpretation, in connection with the role of the Plücker coordinates.

If one takes a straight line as the basic object in 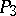, the geometry of this space can be considered as the geometry on the absolute of .

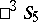The group of projective transformations of 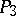is isomorphic to the group of displacements of 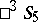, and any involutory projective transformation of 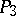corresponds to an involutory displacement in 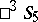. For example, a null system in 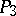corresponds to a reflection in a point and its polar hyperplane in 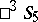; an involutory homology in 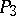corresponds to a hyperbolic paratactic displacement by a half-line in 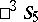, etc. Each connected component of the group of projective transformations for 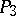corresponds to a connected component of the group of displacements for .

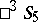1) A collineation of 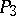with positive determinant, including the identity transformation, corresponds to a displacement in 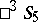with determinant 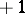(identity transformations are included here).

2) Any correlation in 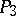with positive determinant (including the null system) corresponds to a displacement in 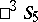with determinant equal to 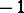that transforms the proper and ideal domains, respectively, into themselves (including reflections in a point).

3) Any collineation of 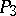having negative determinant corresponds to a displacement in 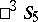with determinant 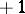that transforms the proper domain into the ideal domain and vice versa, and this component contains a hyperbolic displacement by a half-line.

4) Any correlation in 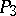having negative determinant corresponds to a displacement in 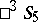with determinant 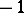that transforms the proper domain into the ideal domain and vice versa.

The images under symmetries that correspond to one another in 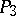and 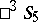are put into correspondence with numerical invariants, between which there are certain relationships.

The Plücker interpretation is used in research on the displacement groups for the three-dimensional non-Euclidean spaces 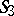, 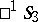and 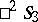, which are isomorphic to certain subgroups of the displacement group for 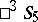. There is also a relation between the groups of motions for these three-dimensional spaces (elliptic and hyperbolic) and groups of displacements of spaces of lower dimensions (see Fubini model; Kotel'nikov interpretation). The Plücker interpretation is also used in examining the interpretation of the three-dimensional symplectic space 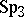in .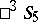

The Plücker interpretation was proposed by J. Plücker [1].

References

[1]	J. Plücker, "Neue Geometrie des Raumes gegründet auf die Betrachtung der geraden Linie als Raumelement" , Teubner (1868)
[2]	B.A. Rozenfel'd, "Non-Euclidean geometry" , Moscow (1955) (In Russian)
[3]	F. Klein, "Vorlesungen über höhere Geometrie" , Springer (1926)

Comments

The quadric in 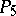whose points represent the lines in 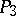is often referred to as the Plücker quadric.

References

[a1]	J.W.P. Hirschfeld, "Finite projective spaces of three dimensions" , Oxford Univ. Press (1985)
[a2]	B.L. van der Waerden, "Einführung in die algebraische Geometrie" , Springer (1939) pp. Chapt. 1
[a3]	D.M.Y. Sommerville, "Analytical geometry of three dimensions" , Cambridge Univ. Press (1934)