Frénet formulas
From Encyclopedia of Mathematics
Revision as of 18:52, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Frénet formulas to Frenet formulas: ascii title)
Formulas that express the derivatives of the unit vectors of the tangent 
, the normal 
and the binormal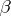 
to a regular curve with respect to the natural parameter 
in terms of these same vectors and the values of the curvature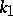 
and torsion 
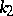of the curve:
 |
 |
 |
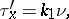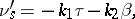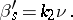They were obtained by F. Frénet (1847).
Comments
References
| [a1] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4 |
How to Cite This Entry:
Frénet formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9net_formulas&oldid=23292
Frénet formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9net_formulas&oldid=23292
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article