De la Vallée-Poussin multiple-point problem
The problem of finding a solution to an ordinary non-linear differential equation of order  ,
,
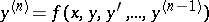 | (1) |
or to a linear equation
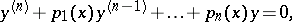 | (2) |
where 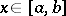 ,
,  ,
, 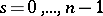 , subject to the conditions
, subject to the conditions
 | (3) |
It was shown by Ch.J. de la Vallée-Poussin [1] that if 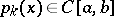 ,
, 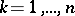 , and if the inequality
, and if the inequality
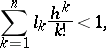 | (4) |
where 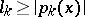 ,
, 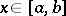 ,
, 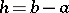 , is met, there exists a unique solution of the problem (2), (3). He also showed that if
, is met, there exists a unique solution of the problem (2), (3). He also showed that if 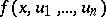 is continuous in all its arguments and satisfies a Lipschitz condition with constant
is continuous in all its arguments and satisfies a Lipschitz condition with constant 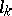 in the variable
in the variable 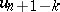 ,
, 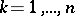 , then, if equation (4) is satisfied, there can be only one solution of the problem (1), (3).
, then, if equation (4) is satisfied, there can be only one solution of the problem (1), (3).
The following aspects of the de la Vallée-Poussin multiple point problem are studied: improvement of an estimate of the number 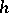 by changing the coefficients of (4); extension of the class of functions
by changing the coefficients of (4); extension of the class of functions 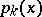 ,
, 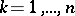 , or
, or 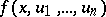 ; and generalization of the conditions (3). A main problem is to prove that the solution exists and that it is unique. As far as the problem (2), (3) is concerned, this is equivalent with the following statement: Any non-trivial solution of equation (2) has at most
; and generalization of the conditions (3). A main problem is to prove that the solution exists and that it is unique. As far as the problem (2), (3) is concerned, this is equivalent with the following statement: Any non-trivial solution of equation (2) has at most 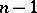 zeros on
zeros on 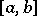 (non-oscillation of solutions or separation of zeros).
(non-oscillation of solutions or separation of zeros).
References
| [1] | Ch.J. de la Vallée-Poussin, "Sur l'equation différentielle linéaire du second ordre. Détermination d'une intégrale par deux valeurs assignées. Extension aux équations d'ordre  " J. Math. Pures Appl. , 8 (1929) pp. 125–144 " J. Math. Pures Appl. , 8 (1929) pp. 125–144 |
| [2] | G. Sansone, "Equazioni differenziali nel campo reale" , 1 , Zanichelli (1948) |
Comments
This problem is also known as the multipoint boundary value problem; it is mostly of historical interest. In [a1] an extension of de la Vallée-Poussin's result is given.
References
| [a1] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
De la Vallée-Poussin multiple-point problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_la_Vall%C3%A9e-Poussin_multiple-point_problem&oldid=23246