Urysohn-Brouwer lemma
Urysohn–Brouwer–Tietze lemma
An assertion on the possibility of extending a continuous function from a subspace of a topological space to the whole space. Let 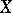 be a normal space and
be a normal space and 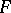 a closed subset of it. Then any continuous function
a closed subset of it. Then any continuous function 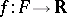 can be extended to a continuous function
can be extended to a continuous function 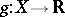 , i.e. one can find a continuous function
, i.e. one can find a continuous function 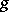 such that
such that 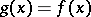 for all
for all 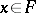 . Moreover, if
. Moreover, if 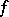 is bounded, then there exists an extension
is bounded, then there exists an extension 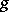 such that
such that
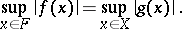 |
The Urysohn–Brouwer lemma was proved by L.E.J. Brouwer and H. Lebesgue for 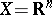 , by H. Tietze for an arbitrary metric space
, by H. Tietze for an arbitrary metric space 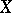 , and by P.S. Urysohn in the above formulation (which may be used as a characterization of normal spaces and is thus best possible).
, and by P.S. Urysohn in the above formulation (which may be used as a characterization of normal spaces and is thus best possible).
References
| [1] | P.S. Urysohn, "Ueber die Mächtigkeit der zusammenhängenden Mengen" Math. Ann. , 94 (1925) pp. 262–295 |
Comments
This assertion is also known as the Tietze–Urysohn extension theorem, or even as the Tietze extension theorem.
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
Urysohn-Brouwer lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Urysohn-Brouwer_lemma&oldid=23095