Riesz-Fischer theorem

A theorem establishing a relationship between the spaces 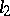and 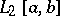: If a system of functions 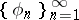is orthonormal on the interval 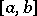(cf. Orthonormal system) and a sequence of numbers 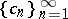is such that

(that is, 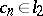), then there exists a function 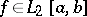for which

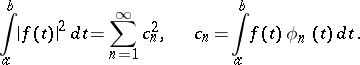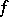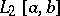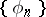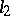Moreover, the function is unique as an element of the space , i.e. up to its values on a set of Lebesgue measure zero. In particular, if the orthonormal system is closed (complete, cf. Complete system of functions) in , then, using the Riesz–Fischer theorem, one gets that the spaces and 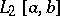are isomorphic and isometric.

The theorem was proved independently by F. Riesz [1] and E. Fischer [2].

References

[1]	F. Riesz, "Sur les systèmes orthogonaux de fonctions" C.R. Acad. Sci. Paris , 144 (1907) pp. 615–619
[2]	E. Fischer, C.R. Acad. Sci. Paris , 144 (1907) pp. 1022–1024; 1148–1150
[3]	I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian)

References

[a1]	R.V. Kadison, J.R. Ringrose, "Fundamentals of the theory of operator algebras" , 1 , Acad. Press (1983)