Poincaré-Bertrand formula
A formula for rearranging the order of integration in iterated improper integrals of Cauchy principal value type (cf. Improper integral).
Let 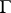 be a simple closed or open smooth curve in the complex plane, let
be a simple closed or open smooth curve in the complex plane, let 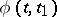 be a function defined on
be a function defined on 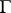 (generally speaking complex-valued) and satisfying a uniform Hölder condition with respect to
(generally speaking complex-valued) and satisfying a uniform Hölder condition with respect to 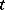 and
and  , and let
, and let 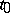 be a fixed point on
be a fixed point on 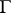 which is not an end-point if
which is not an end-point if 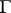 is open. Then one has the Poincaré–Bertrand formula
is open. Then one has the Poincaré–Bertrand formula
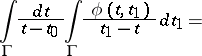 | (1) |
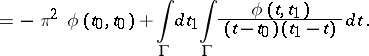 |
The formula is true under more general assumptions on the curve 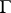 and the function
and the function 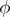 (see [4]). If
(see [4]). If 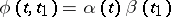 , where
, where 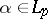 ,
, 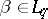 ,
, 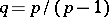 , equation (1) is true for almost-all
, equation (1) is true for almost-all 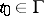 (see [5], [6]). If the curve
(see [5], [6]). If the curve 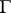 is closed and the function
is closed and the function 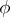 depends on one variable only, then equation (1) takes the form
depends on one variable only, then equation (1) takes the form
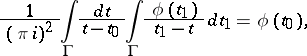 | (2) |
and holds for all or almost-all 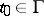 , depending (respectively) on whether
, depending (respectively) on whether 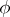 satisfies a Hölder condition or
satisfies a Hölder condition or 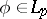 ,
,  . Equation (2) is also called the Poincaré–Bertrand formula.
. Equation (2) is also called the Poincaré–Bertrand formula.
Analogues of formula (1) have been constructed for multiple integrals (see [8]–[11]).
Formula (1) was obtained, under certain conditions, by G.H. Hardy (see [7]) before H. Poincaré (see [1]) and G. Bertrand (see [2], [3]).
References
| [1] | H. Poincaré, "Les méthodes nouvelles de la mécanique céleste" , 3 , Gauthier-Villars (1899) |
| [2] | G. Bertrand, "Equations de Fredholm à intégrales principales au sens de Cauchy" C.R. Acad. Sci. Paris , 172 (1921) pp. 1458–1461 |
| [3] | G. Bertrand, "La théorie des marées et les équations intégrales" Ann. Sci. Ecole Norm. Sup. , 40 (1923) pp. 151–258 |
| [4] | N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
| [5] | B.V. Khvedelidze, "Some properties of singular integrals in the sense of the Cauchy–Lebesgue principal value" Soobsh. Akad. Nauk. GruzSSR , 8 : 5 (1947) pp. 283–290 (In Russian) |
| [6] | B.V. Khvedelidze, "The method of Cauchy-type integrals in the discontinuous boundary-value problems of the theory of holomorphic functions of a complex variable" J. Soviet Math. , 7 : 3 (1977) pp. 309–415 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 7 (1975) pp. 5–162 |
| [7] | G.H. Hardy, "The theory of Cauchy's principal values" Proc. London Math. Soc. , 7 : 2 (1909) pp. 181–208 |
| [8] | F. Tricomi, "Equazioni integrali contenenti il valor principale doppio" Math. Z. , 27 (1928) pp. 87–133 |
| [9] | G. Giraud, "Sur une classe générale d'équations à intégrales principales" C.R. Acad. Sci. Paris , 202 : 26 (1936) pp. 2124–2127 |
| [10] | G. Giraud, "Equations à intégrales principales; étude suivie d'une application" Ann. Sci. Ecole Norm. Sup. , 51 : 3–4 (1934) pp. 251–372 |
| [11] | S.G. Mikhlin, "Singular integral equations" Uspekhi Mat. Nauk , 3 : 3 (1948) pp. 29–112 (In Russian) |
| [12] | S.G. Mikhlin, "Multidimensional singular integrals and integral equations" , Pergamon (1965) (Translated from Russian) |
Poincaré-Bertrand formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poincar%C3%A9-Bertrand_formula&oldid=22913