Pearl-Verhulst logistic process

Verhulst–Pearl logistic process

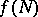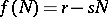In many biological situations the finiteness of available resource means that an isolated population cannot grow without limit, so one may suppose that the net individual growth rate, , is a decreasing function of the population size . The simplest assumption to make is that , whence the deterministic rate of increase

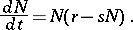(a1)

This defines the Verhulst–Pearl logistic equation, where denotes the intrinsic rate of natural increase for growth with unlimited resources and is the carrying capacity. Integrating (a1) with 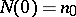yields the solution

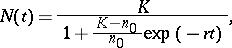(a2)

though a neater representation is

(a3)

since is the time taken for the population to reach half its maximum size . The population therefore initially rises exponentially, followed by a roughly linear phase, before growth tails off towards the asymptote .

Though P.F. Verhulst [a1] introduced the logistic curve in 1838, its use was virtually ignored until R. Pearl and L.J. Reed [a2] rediscovered it empirically in 1920, closely followed by a rational explanation by A.J. Lotka [a3]; further early references are contained in [a4]. A full review is provided in [a5], including a discussion of several logistic-type data sets. Although for many populations the simple linear argument cannot hold, population growth often closely follows the logistic curve (e.g., the population of the USA from 1790 to 1920) even when the underlying assumptions are violated. This has wrongly given it the credence of a universal law.

In contrast, some data sets show an initial logistic rise towards the asymptote 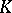, but then fluctuate about it thereafter. Such behaviour can be described by the associated stochastic process with birth and death rates and 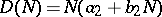, respectively (cf. also Birth-and-death process), for non-negative constants . The corresponding deterministic equation 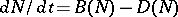reduces to (a1), provided and . Conditional on extinction not having occurred, the equilibrium probabilities (see [a5]) are given by and

(a4)

for . Stochastic simulation is straightforward, since for independent uniformly -distributed random variables , the next event is a birth if and is a death if not, whilst the inter-event time is . Studies show that unless is small, extinction is only likely to occur in the medium term if , i.e. if the individual birth rate increases with .

References

[a1]	P.F. Verhulst, "Notice sur la loi que la population suit dans son accroissement" Corr. Math. et Phys. publ. par A. Quetelet , X (1838) pp. 113–21
[a2]	R. Pearl, L.J. Reed, "On the rate of growth of the population of the United States since 1790 and its mathematical representation" Proc. Nat. Acad. Sci. , 6 (1920) pp. 275–88
[a3]	A.J. Lotka, "Elements of physical biology" , Williams and Wilkins (1925)
[a4]	R. Pearl, "Introduction of medical biometry and statistics" , Saunders (1930)
[a5]	E. Renshaw, "Modelling biological populations in space and time" , Cambridge Univ. Press (1991)