Orr-Sommerfeld equation
A linear ordinary differential equation
 | (1) |
where 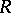 is the Reynolds number,
is the Reynolds number, 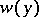 is a given function (the profile of the velocity of the undisturbed flow) which is usually taken to be holomorphic in a neighbourhood of the segment
is a given function (the profile of the velocity of the undisturbed flow) which is usually taken to be holomorphic in a neighbourhood of the segment 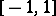 in the complex
in the complex 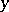 -plane,
-plane, 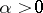 is constant, and
is constant, and  is a spectral parameter. For the Orr–Sommerfeld equation, the boundary value problem
is a spectral parameter. For the Orr–Sommerfeld equation, the boundary value problem
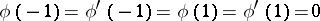 | (2) |
is examined. The Orr–Sommerfeld equation arose from the research by W. Orr
and A. Sommerfeld [2] concerning the stability in a linear approximation of a plane Poiseuille flow — a flow of a viscous incompressible liquid in a tube 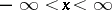 ,
, 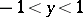 , with rigid boundaries; for the stream function, the disturbance takes the form
, with rigid boundaries; for the stream function, the disturbance takes the form 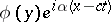 .
.
The eigen values of the problem (1), (2), generally speaking, are complex; the flow is stable if 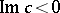 for all eigen values, and unstable if
for all eigen values, and unstable if 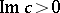 for some of them. The curve
for some of them. The curve 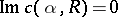 is called a neutral curve. The Poiseuille flow is stable for small Reynolds numbers. W. Heisenberg [6] was the first to propose that a Poiseuille flow is unstable for large Reynolds numbers, and calculated four points of the neutral curve. For a quadratic profile of velocity, it has been established that the flow is unstable for
is called a neutral curve. The Poiseuille flow is stable for small Reynolds numbers. W. Heisenberg [6] was the first to propose that a Poiseuille flow is unstable for large Reynolds numbers, and calculated four points of the neutral curve. For a quadratic profile of velocity, it has been established that the flow is unstable for  .
.
The asymptotic theory of the Orr–Sommerfeld equation is based on the assumption that 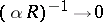 is a small parameter. A point
is a small parameter. A point 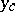 at which
at which 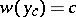 is a turning point (see Small parameter, method of the). The appropriate parameter is
is a turning point (see Small parameter, method of the). The appropriate parameter is 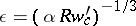 . In the local coordinates
. In the local coordinates 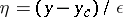 the equation becomes
the equation becomes 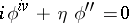 , with a solution of the form
, with a solution of the form
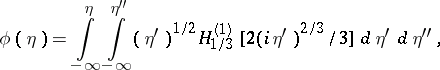 |
which is valid for 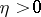 . In general, at a finite distance from
. In general, at a finite distance from 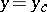 one obtains a fundamental system of solutions of the form
one obtains a fundamental system of solutions of the form
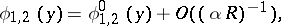 |
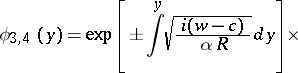 |
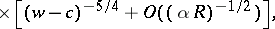 |
where 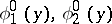 is a fundamental system of solutions of the non-viscous (i.e.
is a fundamental system of solutions of the non-viscous (i.e. 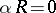 ) equation
) equation
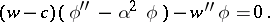 |
Research into the problem (1), (2) entails, among others, the following difficulties: 1) the non-viscous equation in a neighbourhood of 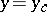 has a holomorphic solution and a solution with a logarithmic singularity; 2) for small
has a holomorphic solution and a solution with a logarithmic singularity; 2) for small 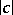 (i.e. in the most important instance) the turning points merge with the end points of the segment
(i.e. in the most important instance) the turning points merge with the end points of the segment 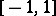 (for example, for a quadratic profile of velocity
(for example, for a quadratic profile of velocity 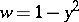 ).
).
When 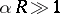 , a strict proof of instability has been obtained (see [3], [4]).
, a strict proof of instability has been obtained (see [3], [4]).
References
| [1a] | W.McF. Orr, "The stability or instability of the steady motions of a liquid I" Proc. R. Irish Acad. A , 27 (1907) pp. 9–68 |
| [1b] | W.McF. Orr, "The stability or instability of the steady motions of a perfect liquid and of a viscous liquid II" Proc. R. Irish Acad. A , 27 (1907) pp. 69–138 |
| [2] | A. Sommerfeld, , Proc. 4-th Internat. Congress of Mathematicians Rome, 1908 (1909) pp. 116–124 |
| [3] | C.C. Lin, "Theory of hydrodynamic stability" , Cambridge Univ. Press (1955) |
| [4] | G. Birkhoff (ed.) et al. (ed.) , Hydrodynamic instability , Proc. Symp. Appl. Math. , 13 , Amer. Math. Soc. (1962) |
| [5] | J.M. Gersting, D.F. Janowski, "Numerical methods for Orr–Sommerfeld problems" Internat. J. Numer. Methods Eng. , 4 (1972) pp. 195–206 |
| [6] | W. Heisenberg, Ann. of Phys. , 74 : 15 (1924) pp. 577–627 |
Comments
See also Poiseuille flow.
References
| [a1] | W.O. Criminale, "Stability of parallel flows" , Acad. Press (1967) |
| [a2] | H. Schlichting, "Fluid dynamics I" S. Flügge (ed.) , Handbuch der Physik , VIII/1 , Springer (1959) pp. 351–450 |
| [a3] | A. Georgescu, "Hydrodynamic stability theory" , M. Nijhoff (1985) |
Orr-Sommerfeld equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orr-Sommerfeld_equation&oldid=22867