Nevanlinna-Pick problem
Given a class  of analytic functions in a domain
of analytic functions in a domain 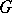 of the complex plane (or, in a more general context, of a Riemann surface), to find necessary and sufficient conditions for the solvability in
of the complex plane (or, in a more general context, of a Riemann surface), to find necessary and sufficient conditions for the solvability in 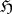 of the interpolation problem
of the interpolation problem
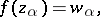 | (1) |
where 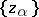 is a subset of
is a subset of 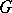 ,
,  is some set of complex numbers, and
is some set of complex numbers, and 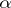 usually runs through a countable (sometimes finite, sometimes even uncountable) index set. The classical result of G. Pick [1] and R. Nevanlinna [2] (for finite and countable subsets
usually runs through a countable (sometimes finite, sometimes even uncountable) index set. The classical result of G. Pick [1] and R. Nevanlinna [2] (for finite and countable subsets  , respectively) yields the solution of this problem, for example, in the class
, respectively) yields the solution of this problem, for example, in the class  of analytic functions in the unit disc that are bounded by 1 in absolute value. The desired condition here is the non-negativity of the quadratic forms
of analytic functions in the unit disc that are bounded by 1 in absolute value. The desired condition here is the non-negativity of the quadratic forms
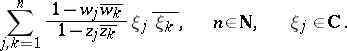 |
The first proof of this proposition (see [3], [4]), as well as quite analogous and similar results for various other function classes  , relied on algebraic and functional-theoretic methods. Later proofs, based, for example, on reducing the Nevanlinna–Pick problem to a moment problem or obtained from the point of view of the theory of Hilbert spaces, have made it possible to extend the result to uncountable subsets
, relied on algebraic and functional-theoretic methods. Later proofs, based, for example, on reducing the Nevanlinna–Pick problem to a moment problem or obtained from the point of view of the theory of Hilbert spaces, have made it possible to extend the result to uncountable subsets 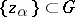 and pointed the way to possible generalizations (see [3]–[5]).
and pointed the way to possible generalizations (see [3]–[5]).
A natural development of the Nevanlinna–Pick problem, which necessitated an appeal to functional-analytic methods of investigation, was the question of the solvability of the interpolation problem (1) on a class 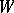 of right-hand sides
of right-hand sides  ; in this case, as a rule,
; in this case, as a rule, 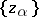 is a countable set (a sequence) of points of
is a countable set (a sequence) of points of 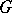 , while
, while 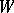 may be one of various spaces of sequences of complex numbers. In connection with the class
may be one of various spaces of sequences of complex numbers. In connection with the class 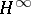 of bounded analytic functions in the unit disc and the space
of bounded analytic functions in the unit disc and the space 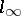 of bounded sequences, a complete description of the corresponding point sequences
of bounded sequences, a complete description of the corresponding point sequences  (known as universal interpolation sequences) has been obtained (see [6]) in the form of the condition
(known as universal interpolation sequences) has been obtained (see [6]) in the form of the condition
 | (2) |
This result played an important role in describing the structure of the maximal ideal space of the algebra  (see [7]) and was at the same time a starting point for extensive research into the Nevanlinna–Pick problem (in the above generalized formulation) for the Hardy classes
(see [7]) and was at the same time a starting point for extensive research into the Nevanlinna–Pick problem (in the above generalized formulation) for the Hardy classes  and the spaces
and the spaces  (including weight spaces). It turned out that when
(including weight spaces). It turned out that when  the solution is independent of
the solution is independent of 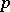 and is given by condition (2), while when
and is given by condition (2), while when  it necessarily varies when
it necessarily varies when 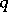 and
and 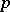 are changed (see ). Another generalization of the Nevanlinna–Pick problem is connected with the interpolation problem
are changed (see ). Another generalization of the Nevanlinna–Pick problem is connected with the interpolation problem 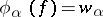 , where
, where  is some system of functionals in a class
is some system of functionals in a class  . The problem of describing the set
. The problem of describing the set 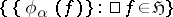 may be regarded as a generalization of the well-known coefficient problem for classes of analytic functions.
may be regarded as a generalization of the well-known coefficient problem for classes of analytic functions.
References
| [1] | G. Pick, "Ueber die Beschränkungen analytischer Funktionen, welche durch vorgegebene Funktionswerte bewirkt werden" Math. Ann. , 77 (1916) pp. 7–23 |
| [2] | R. Nevanlinna, "Ueber beschränkte analytische Funktionen" Ann. Acad. Sci. Fenn. Ser. A , 32 : 7 (1929) pp. 1–15 |
| [3] | M.G. Krein, A.A. Nudel'man, "The Markov moment problem and extremal problems" , Amer. Math. Soc. (1977) (Translated from Russian) |
| [4] | J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981) |
| [5] | B. Sz.-Nagy, A. Korányi, "Rélations d'un problem de Nevanlinna et Pick avec la théorie des opérateurs de l'espace Hilbertien" Acta Math. Acad. Sci. Hung. , 7 (1956) pp. 295–303 |
| [6] | L. Carleson, "An interpolation problem for bounded analytic functions" Amer. J. Math. , 80 : 4 (1958) pp. 921–930 |
| [7] | S.V. Shvedenko, "On 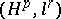 -interpolation sequences in the unit disk" Math. USSR Sb. , 46 : 4 (1983) pp. 473–492 Mat. Sb. , 118 : 4 (1982) pp. 470–489 -interpolation sequences in the unit disk" Math. USSR Sb. , 46 : 4 (1983) pp. 473–492 Mat. Sb. , 118 : 4 (1982) pp. 470–489 |
Comments
This classical topic was reactivated and extended to matrix-valued functions in the 1960s and the beginning of the 1970s. Connections with operator theory became essential in the new developments (see, e.g., [a1]–[a3]). Applications to problems in control theory, which appeared in the 1980s, required a revision of the theory and the development of computational methods, in particular, for rational matrix functions (see [a4], [a5]).
See also  control theory.
control theory.
References
| [a1] | V.M. [V.M. Adamyan] Adamjan, D.Z. Arov, M.G. Krein, "Analytic properties of Schmidt pairs for a Hankel operator and the generalized Schur–Tagaki problem" Math. USSR Sb. , 15 (1971) pp. 31–73 Mat. Sb. , 86 : 1 (1971) pp. 34–75 |
| [a2] | M. Rosenblum, J. Rovnyak, "Hardy classes and operator theory" , Oxford Univ. Press (1985) |
| [a3] | D. Sarason, "Operator-theoretic aspects of the Nevanlinna–Pick interpolation problem" S.C. Power (ed.) , Operators and function theory , Reidel (1984) pp. 279–314 |
| [a4] | H. Kimura, "Directional interpolation approach in 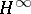 -optimization" IEEE Trans. Autom. Control , 32 (1987) pp. 1085–1093 -optimization" IEEE Trans. Autom. Control , 32 (1987) pp. 1085–1093 |
| [a5] | D.J.N. Limebeer, B.D.O. Anderson, "An interpolation theory approach to 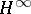 controller degree bounds" Linear Algebra Appl. , 98 (1988) pp. 347–386 controller degree bounds" Linear Algebra Appl. , 98 (1988) pp. 347–386 |
| [a6] | J.A. Ball, "Nevanlinna–Pick interpolation: Generalizations and applications" J.B. Conway (ed.) , Proc. Asymmetric Algebras and Invariant Subspaces. Conf. Indian Univ. , Pitman (To appear) |
| [a7] | H. Dym, "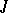 contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , Amer. Math. Soc. (1989) contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , Amer. Math. Soc. (1989) |
| [a8] | J.W. Helton, "Operator theory, analytic functions, matrices, and electrical engineering" , Amer. Math. Soc. (1987) |
| [a9] | P.L. Duren, "Theory of 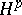 spaces" , Acad. Press (1970) spaces" , Acad. Press (1970) |
Nevanlinna-Pick problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nevanlinna-Pick_problem&oldid=22839