Mehler–Fok transform
The integral transform
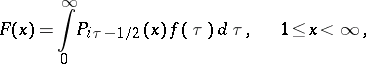 | (1) |
where 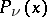 is the Legendre function of the first kind (cf. Legendre functions). If
is the Legendre function of the first kind (cf. Legendre functions). If 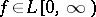 , the function
, the function 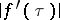 is locally integrable on
is locally integrable on 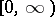 and
and 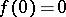 , then the following inversion formula is valid:
, then the following inversion formula is valid:
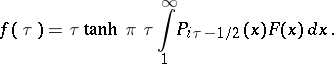 | (2) |
The Parseval identity. Consider the Mehler–Fock transform and its inverse defined by the equalities
If 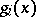 ,
, 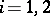 , are arbitrary real-valued functions satisfying the conditions
, are arbitrary real-valued functions satisfying the conditions
then
The generalized Mehler–Fock transform and the corresponding inversion formula are:
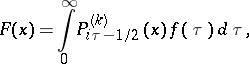 | (3) |
and
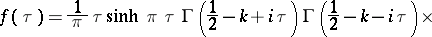 | (4) |
where 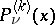 are the associated Legendre functions of the first kind. For
are the associated Legendre functions of the first kind. For 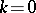 formulas (3) and (4) reduce to (1) and (2); for
formulas (3) and (4) reduce to (1) and (2); for 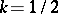 ,
, 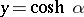 , formulas (3) and (4) lead to the Fourier cosine transform, and for
, formulas (3) and (4) lead to the Fourier cosine transform, and for 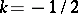 ,
, 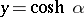 to the Fourier sine transform. The transforms (1) and (2) were introduced by F.G. Mehler [1]. The basic theorems were proved by V.A. Fock [V.A. Fok].
to the Fourier sine transform. The transforms (1) and (2) were introduced by F.G. Mehler [1]. The basic theorems were proved by V.A. Fock [V.A. Fok].
References
| [1] | F.G. Mehler, "Ueber eine mit den Kugel- und Cylinderfunctionen verwandte Function und ihre Anwendung in der Theorie der Electricitätsvertheilung" Math. Ann. , 18 (1881) pp. 161–194 |
| [2] | V.A. Fok, "On the representation of an arbitrary function by an integral involving Legendre functions with complex index" Dokl. Akad. Nauk SSSR , 39 (1943) pp. 253–256 (In Russian) |
| [3] | V.A. Ditkin, A.P. Prudnikov, "Operational calculus" Progress in Math. , 1 (1968) pp. 1–75 Itogi Nauk. Mat. Anal. 1966 (1967) pp. 7–82 |
References
| [a1] | I.N. Sneddon, "The use of integral transforms" , McGraw-Hill (1972) |
How to Cite This Entry:
Mehler-Fock transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mehler-Fock_transform&oldid=22805
This article was adapted from an original article by Yu.A. BrychkovA.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article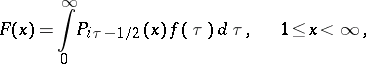
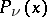 is the Legendre function of the first kind (cf. Legendre functions). If
is the Legendre function of the first kind (cf. Legendre functions). If 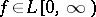 , the function
, the function 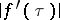 is locally integrable on
is locally integrable on 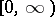 and
and 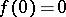 , then the following inversion formula is valid:
, then the following inversion formula is valid:
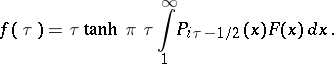
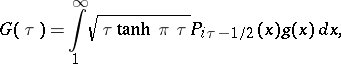
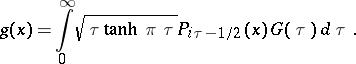
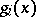 ,
, 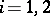 , are arbitrary real-valued functions satisfying the conditions
, are arbitrary real-valued functions satisfying the conditions
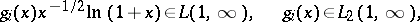
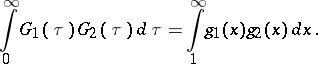
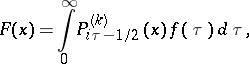
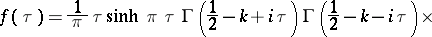
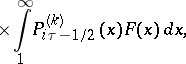
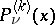 are the associated Legendre functions of the first kind. For
are the associated Legendre functions of the first kind. For 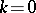 formulas (3) and (4) reduce to (1) and (2); for
formulas (3) and (4) reduce to (1) and (2); for 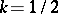 ,
, 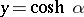 , formulas (3) and (4) lead to the Fourier cosine transform, and for
, formulas (3) and (4) lead to the Fourier cosine transform, and for 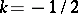 ,
, 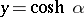 to the Fourier sine transform. The transforms (1) and (2) were introduced by F.G. Mehler [1]. The basic theorems were proved by V.A. Fock [V.A. Fok].
to the Fourier sine transform. The transforms (1) and (2) were introduced by F.G. Mehler [1]. The basic theorems were proved by V.A. Fock [V.A. Fok].