Kähler form

The fundamental form of a Kähler metric on a complex manifold. A Kähler form is a harmonic real differential form of type 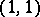. A differential form 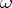on a complex manifold 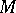is the Kähler form of a Kähler metric if and only if every point 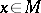has a neighbourhood 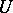in which

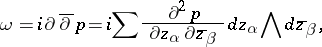where 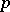is a strictly plurisubharmonic function in 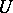and are complex local coordinates.

A Kähler form is called a Hodge form if it corresponds to a Hodge metric, i.e. if it has integral periods or, equivalently, defines an integral cohomology class.

References

[1]	R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980)

Comments

For fundamental form of a Kähler metric see Kähler metric.

References

[a1]	A. Weil, "Introduction à l'Aeetude des variétés kahlériennes" , Hermann (1958)