Fourier-Borel transform
Let 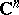 be the
be the  -dimensional complex space, and let
-dimensional complex space, and let 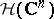 denote the space of entire functions in
denote the space of entire functions in  complex variables, equipped with the topology of uniform convergence on the compact subsets of
complex variables, equipped with the topology of uniform convergence on the compact subsets of 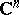 (cf. also Entire function; Uniform convergence). Let
(cf. also Entire function; Uniform convergence). Let 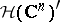 be its dual space of continuous linear functionals. The elements of
be its dual space of continuous linear functionals. The elements of 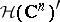 are usually called analytic functionals in
are usually called analytic functionals in 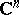 .
.
One says that a compact set  is a carrier for an analytic functional
is a carrier for an analytic functional 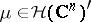 if for every open neighbourhood
if for every open neighbourhood 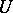 of
of 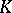 there exists a positive constant
there exists a positive constant 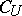 such that, for every
such that, for every 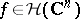 ,
,
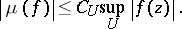 |
General references for these notions are [a3], [a5].
Let 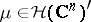 . The Fourier–Borel transform
. The Fourier–Borel transform 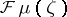 is defined by
is defined by
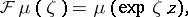 |
where 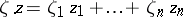
For 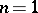 , the use of this transform goes back to E. Borel, while for
, the use of this transform goes back to E. Borel, while for 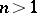 it first appeared in a series of papers by A. Martineau, culminating with [a6].
it first appeared in a series of papers by A. Martineau, culminating with [a6].
It is immediate to show that 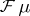 is an entire function. Moreover, since the exponentials are dense in
is an entire function. Moreover, since the exponentials are dense in 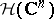 , an analytic functional is uniquely determined by its Fourier–Borel transform.
, an analytic functional is uniquely determined by its Fourier–Borel transform.
By using the definition of carrier of an analytic functional, it is easy to see that if 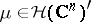 is carried by a compact convex set
is carried by a compact convex set 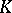 , then for every
, then for every 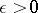 there exists a number
there exists a number 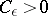 such that, for any
such that, for any 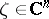 ,
,
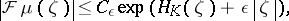 |
where 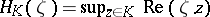 is the support function of
is the support function of 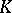 .
.
A fundamental result in the theory of the Fourier–Borel transform is the fact that the converse is true as well: Let 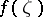 be an entire function. Suppose that for some compact convex set
be an entire function. Suppose that for some compact convex set 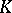 and for every
and for every 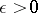 there exists a number
there exists a number 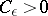 such that, for any
such that, for any 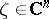 ,
,
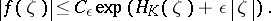 | (a1) |
Then 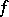 is the Fourier–Borel transform of an analytic functional
is the Fourier–Borel transform of an analytic functional 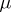 carried by
carried by 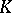 .
.
This theorem, for 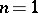 , was proved by G. Pólya, while for
, was proved by G. Pólya, while for 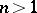 it is due to A. Martineau [a7].
it is due to A. Martineau [a7].
In particular, the Fourier–Borel transform establishes an isomorphism between the space 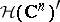 and the space
and the space 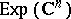 of entire functions of exponential type, i.e. those entire functions
of entire functions of exponential type, i.e. those entire functions 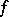 for which there are positive constants
for which there are positive constants 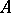 ,
, 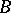 such that
such that
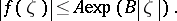 |
If 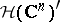 is endowed with the strong topology, and
is endowed with the strong topology, and 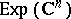 with its natural inductive limit topology, then the Fourier–Borel transform is actually a topological isomorphism, [a2].
with its natural inductive limit topology, then the Fourier–Borel transform is actually a topological isomorphism, [a2].
A case of particular interest occurs when, in the above assertion, one takes 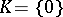 . In this case, a function which satisfies the estimate (a1), i.e.
. In this case, a function which satisfies the estimate (a1), i.e.
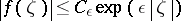 |
is said to be of exponential type zero, or of infra-exponential type. Given such a function 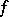 , there exists a unique analytic functional
, there exists a unique analytic functional  such that
such that 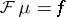 ; such a functional is carried by
; such a functional is carried by  and therefore is a continuous linear functional on any space
and therefore is a continuous linear functional on any space 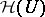 , for
, for 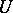 an open subset of
an open subset of 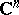 containing the origin. If one denotes by
containing the origin. If one denotes by 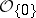 the space of germs of holomorphic functions at the origin (cf. also Germ), then
the space of germs of holomorphic functions at the origin (cf. also Germ), then 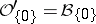 , the space of hyperfunctions supported at the origin (cf. also Hyperfunction); the Fourier–Borel transform is therefore well defined on such a space. In fact, it is well defined on every hyperfunction with compact support. For this and related topics, see e.g. [a1], [a4].
, the space of hyperfunctions supported at the origin (cf. also Hyperfunction); the Fourier–Borel transform is therefore well defined on such a space. In fact, it is well defined on every hyperfunction with compact support. For this and related topics, see e.g. [a1], [a4].
The Fourier–Borel transform is a central tool in the study of convolution equations in convex sets in 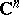 . As an example, consider the problem of surjectivity. Let
. As an example, consider the problem of surjectivity. Let  be an open convex subset of
be an open convex subset of 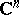 and let
and let 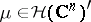 be carried by a compact set
be carried by a compact set 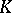 . Then the convolution operator
. Then the convolution operator
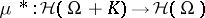 |
is defined by
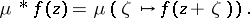 |
One can show (see [a5] or [a1] and the references therein) that if 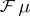 is of completely regular growth and the radial regularized indicatrix of
is of completely regular growth and the radial regularized indicatrix of 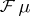 coincides with
coincides with 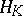 , then
, then 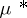 is a surjective operator. The converse is true provided that
is a surjective operator. The converse is true provided that  is bounded, strictly convex, with
is bounded, strictly convex, with 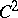 boundary.
boundary.
References
| [a1] | C.A. Berenstein, D.C. Struppa, "Complex analysis and convolution equations" , Encycl. Math. Sci. , 54 , Springer (1993) pp. 1–108 |
| [a2] | L. Ehrenpreis, "Fourier analysis in several complex variables" , Wiley (1970) |
| [a3] | L. Hörmander, "An introduction to complex analysis in several variables" , v. Nostrand (1966) |
| [a4] | G. Kato, D.C. Struppa, "Fundamentals of algebraic microlocal analysis" , M. Dekker (1999) |
| [a5] | P. Lelong, L. Gruman, "Entire functions of several complex variables" , Springer (1986) |
| [a6] | A. Martineau, "Sur les fonctionnelles analytiques et la transformation de Fourier–Borel" J. Ann. Math. (Jerusalem) , XI (1963) pp. 1–164 |
| [a7] | A. Martineau, "Equations différentialles d'ordre infini" Bull. Soc. Math. France , 95 (1967) pp. 109–154 |
Fourier-Borel transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier-Borel_transform&oldid=22441