Fishburn-Shepp inequality
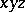inequality
An inequality for linear extensions of a finite partially ordered set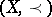 
. Elements 
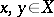are incomparable if 
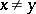and neither 
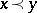nor 
. Denote by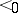 
a generic linear order extension of 
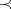on 
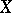, let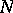 
be the number of linear extensions 
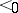, and let 
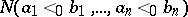be the number of linear extensions in which 
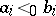for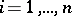 
.
The Fishburn–Shepp inequality says that if 
, 
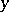and 
are mutually incomparable members of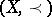 
, then
 |
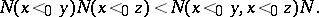This was first proved for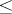 
in [a3], then for 
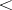in [a2]. The Ahlswede–Daykin inequality [a1] plays a key role in the proof.
The inequality is also written as
 |
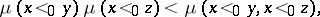where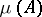 
denotes the probability that a randomly chosen linear extension 
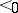of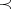 
satisfies 
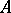. When written as 
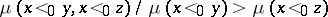, one sees that the probability of 
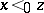increases when it is true that also 
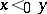. Some plausible related inequalities are false [a3].
See also Correlation inequalities; FKG inequality; Holley inequality.
References
| [a1] | R. Ahlswede, D.E. Daykin, "An inequality for the weights of two families, their unions and intersections" Z. Wahrscheinlichkeitsth. verw. Gebiete , 43 (1978) pp. 183–185 |
| [a2] | P.C. Fishburn, "A correlational inequality for linear extensions of a poset" Order , 1 (1984) pp. 127–137 |
| [a3] | L.A. Shepp, "The XYZ conjecture and the FKG inequality" Ann. of Probab. , 10 (1982) pp. 824–827 |
Fishburn-Shepp inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fishburn-Shepp_inequality&oldid=22427