Cartan-Weyl basis
of a finite-dimensional semi-simple complex Lie algebra 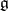
A basis of 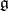 consisting of elements of a Cartan subalgebra
consisting of elements of a Cartan subalgebra  of
of 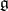 and root vectors
and root vectors 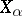 ,
, 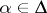 , where
, where 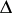 is the system of all non-zero roots of
is the system of all non-zero roots of 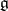 with respect to
with respect to 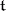 . The choice of a Cartan–Weyl basis is not unique. A root
. The choice of a Cartan–Weyl basis is not unique. A root 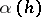 ,
, 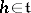 , is identified, as a linear form on
, is identified, as a linear form on 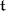 , with the vector
, with the vector 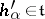 such that
such that 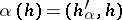 , where
, where 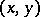 is the Killing form in
is the Killing form in 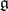 . Here
. Here
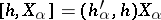 |
for each 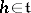 . If
. If 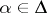 , then
, then 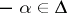 and the root vectors
and the root vectors 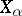 can be chosen such that
can be chosen such that 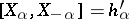 . If
. If 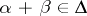 , then
, then
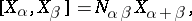 |
where 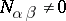 . If
. If 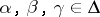 ,
, 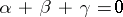 , then
, then 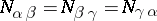 . There exists a normalization of the vectors
. There exists a normalization of the vectors 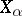 for which
for which 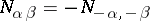 , where the numbers
, where the numbers 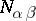 obtained are rational. There exists a normalization of the vectors
obtained are rational. There exists a normalization of the vectors 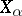 under which all
under which all 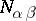 are integers (see Chevalley group). The definition of a Cartan–Weyl basis (introduced by H. Weyl in [1]), as well as everything mentioned above concerning the vectors
are integers (see Chevalley group). The definition of a Cartan–Weyl basis (introduced by H. Weyl in [1]), as well as everything mentioned above concerning the vectors 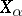 ,
, 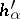 and the numbers
and the numbers 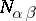 , carry over verbatim to the case of an arbitrary finite-dimensional split semi-simple Lie algebra over a field of characteristic zero and its root decomposition with respect to a split Cartan subalgebra.
, carry over verbatim to the case of an arbitrary finite-dimensional split semi-simple Lie algebra over a field of characteristic zero and its root decomposition with respect to a split Cartan subalgebra.
References
| [1] | H. Weyl, "Theorie der Darstellung kontinuierlicher halb-einfacher Gruppen durch lineare Transformationen I" Math. Z. , 23 (1925) pp. 271–309 |
| [2] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [3] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
Comments
See also Lie algebra, semi-simple for a description of the special case of a Chevalley basis.
References
| [a1] | J.-P. Serre, "Algèbres de Lie semi-simples complexes" , Benjamin (1966) |
| [a2] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 |
| [a3] | R.W. Carter, "Simple groups of Lie type" , Wiley (Interscience) (1972) |
Cartan-Weyl basis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartan-Weyl_basis&oldid=22255