Bellman-Gronwall inequality
An assertion which deduces from a linear integral inequality (cf. also Differential inequality)
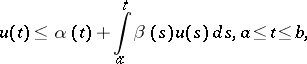 | (a1) |
where  ,
, 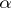 are real continuous functions on the interval
are real continuous functions on the interval 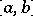 and the function
and the function 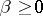 is integrable on
is integrable on 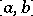 , an inequality for the unknown function
, an inequality for the unknown function  :
:
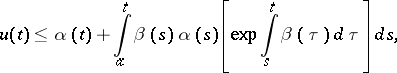 | (a2) |
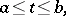 |
To prove this assertion, it suffices to establish (see [a1]) that the integral in (a1) does not exceed the integral in (a2).
A less general form of the Bellman–Gronwall inequality is as follows: If the function 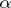 is non-decreasing (or constant, in particular), then
is non-decreasing (or constant, in particular), then
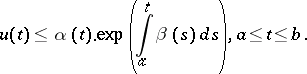 |
The Bellman–Gronwall inequality can be used to estimate the solution of a linear non-homogeneous (or non-linear) ordinary differential equation in terms of the initial condition and the non-homogeneity (or non-linearity). This allows one to establish the existence and stability of the solution. This inequality can be also used to justify the averaging method, namely to estimate the difference between the solutions of the initial equation and the averaged one.
There is a generalization of the Bellman–Gronwall inequality to the case of a piecewise-continuous function  satisfying for
satisfying for 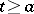 the inequality
the inequality
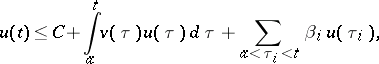 |
where 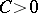 ,
, 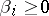 ,
, 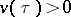 , and
, and 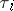 are the points of discontinuity of the function
are the points of discontinuity of the function 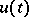 . Then
. Then 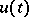 satisfies the estimate (see [a2]):
satisfies the estimate (see [a2]):
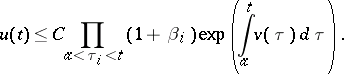 |
This form of the inequality plays the same role in the theory of differential equations with impulse effect, as the usual form of the inequality does in the theory of ordinary differential equations.
References
| [a1] | J. Hale, "Theory of functional differential equations" , Springer (1977) |
| [a2] | A. Samoilenko, N. Perestyuk, "Impulsive differential equations" , World Sci. (1995) (In Russian) |
Bellman-Gronwall inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bellman-Gronwall_inequality&oldid=22081