Behnke-Stein theorem
From Encyclopedia of Mathematics
The union of domains of holomorphy 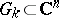 ,
,  for which
for which 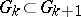 for all
for all 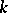 , is also a domain of holomorphy. The Behnke–Stein theorem is valid not only in the complex Euclidean space
, is also a domain of holomorphy. The Behnke–Stein theorem is valid not only in the complex Euclidean space  , but also on any Stein manifold. If the sequence
, but also on any Stein manifold. If the sequence 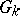 is not monotone increasing by imbedding, the theorem is not valid; e.g. the union of the two domains of holomorphy
is not monotone increasing by imbedding, the theorem is not valid; e.g. the union of the two domains of holomorphy
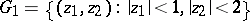 |
and
 |
in 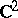 is not a domain of holomorphy.
is not a domain of holomorphy.
References
| [1] | H. Behnke, K. Stein, "Konvergente Folgen von Regularitätsbereichen und die Meromorphiekonvexität" Math. Ann. , 116 (1938) pp. 204–216 |
| [2] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
How to Cite This Entry:
Behnke-Stein theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Behnke-Stein_theorem&oldid=22077
Behnke-Stein theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Behnke-Stein_theorem&oldid=22077
This article was adapted from an original article by E.M. Chirka (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article