Relative root system

of a connected reductive algebraic group defined over a field

A system of non-zero weights of the adjoint representation of a maximal -split torus of the group in the Lie algebra of this group (cf. Weight of a representation of a Lie algebra). The weights themselves are called the roots of relative to . The relative root system , which can be seen as a subset of its linear envelope 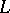in the space 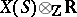, where is the group of rational characters of the torus 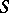, is a root system. Let 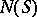be the normalizer and the centralizer of in . Then is the connected component of the unit of the group ; the finite group 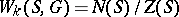is called the Weyl group of over 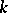, or the relative Weyl group. The adjoint representation of in 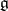defines a linear representation of 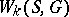in . This representation is faithful and its image is the Weyl group of the root system , which enables one to identify these two groups. 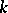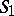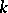Since two maximal -split tori and in are conjugate over , the relative root systems 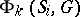and the relative Weyl groups , , are isomorphic, respectively. Hence they are often denoted simply by and 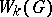. When is split over , the relative root system and the relative Weyl group coincide, respectively, with the usual (absolute) root system and Weyl group of 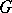. Let 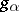be the weight subspace in relative to 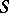, corresponding to the root 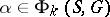. If is split over , then 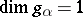for any , and is a reduced root system; this is not so in general: does not have to be reduced and 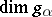can be greater than 1. The relative root system 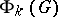is irreducible if is simple over .

The relative root system plays an important role in the description of the structure and in the classification of semi-simple algebraic groups over 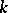. Let be semi-simple, and let be a maximal torus defined over 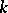and containing 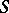. Let and be the groups of rational characters of the tori and 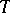with fixed compatible order relations, let be a corresponding system of simple roots of relative to 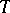, and let 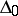be the subsystem in consisting of the characters which are trivial on 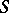. Moreover, let 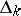be the system of simple roots in the relative root system defined by the order relation chosen on 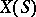; it consists of the restrictions to of the characters of the system 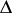. The Galois group 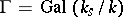acts naturally on , and the set 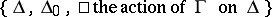is called the 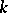-index of the semi-simple group . 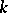The role of the -index is explained by the following theorem: Every semi-simple group over is uniquely defined, up to a 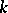-isomorphism, by its class relative to an isomorphism over 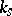, its 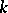-index and its anisotropic kernel. 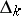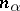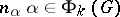The relative root system is completely defined by the system and by the set of natural numbers , (equal to 1 or 2), such that but 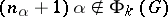. Conversely, 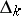and , , 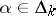can be determined from the 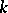-index. In particular, two elements from 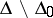have one and the same restriction to 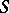if and only if they are located in the same orbit of 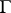; this defines a bijection between 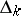and the set of orbits of 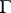into .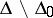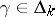

If , if 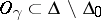is the corresponding orbit, if is any connected component in 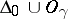not all vertices of which lie in 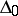, then 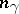is the sum of the coefficients of the roots 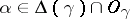in the decomposition of the highest root of the system 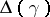in simple roots.

If 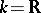, , 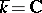then the above relative root system and relative Weyl group are naturally identified with the root system and Weyl group, respectively, of the corresponding symmetric space.

References

[1]	J. Tits, "Sur la classification des groupes algébriques semi-simples" C.R. Acad. Sci. Paris , 249 (1959) pp. 1438–1440
[2]	A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150
[3]	J. Tits, "Classification of algebraic simple groups" , Algebraic Groups and Discontinuous Subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 33–62