Cohomology with coefficients in a non-Abelian group, a sheaf of non-Abelian groups, etc. The best known examples are the cohomology of groups, topological spaces and the more general example of the cohomology of sites (i.e. topological categories; cf. Topologized category) in dimensions 0, 1. A unified approach to non-Abelian cohomology can be based on the following concept. Let  ,
, 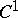 be groups, let
be groups, let  be a set with a distinguished point
be a set with a distinguished point  , let
, let  be the holomorph of
be the holomorph of  (i.e. the semi-direct product of
(i.e. the semi-direct product of  and
and 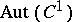 ; cf. also Holomorph of a group), and let
; cf. also Holomorph of a group), and let  be the group of permutations of
be the group of permutations of  that leave
that leave  fixed. Then a non-Abelian cochain complex is a collection
fixed. Then a non-Abelian cochain complex is a collection
where 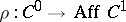 ,
, 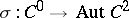 are homomorphisms and
are homomorphisms and  is a mapping such that
is a mapping such that
Define the  -dimensional cohomology group by
-dimensional cohomology group by
and the  -dimensional cohomology set (with distinguished point) by
-dimensional cohomology set (with distinguished point) by
where 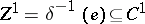 and the factorization is modulo the action
and the factorization is modulo the action  of the group
of the group  .
.
Examples.
1) Let  be a topological space with a sheaf of groups
be a topological space with a sheaf of groups  , and let
, and let  be a covering of
be a covering of  ; one then has the Čech complex
; one then has the Čech complex
where 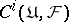 are defined as in the Abelian case (see Cohomology),
are defined as in the Abelian case (see Cohomology),
Taking limits with respect to coverings, one obtains from the cohomology sets 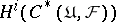 ,
,  , the cohomology
, the cohomology 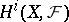 ,
, 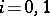 , of the space
, of the space 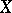 with coefficients in
with coefficients in 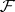 . Under these conditions,
. Under these conditions, 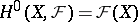 . If
. If 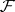 is the sheaf of germs of continuous mappings with values in a topological group
is the sheaf of germs of continuous mappings with values in a topological group 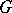 , then
, then  can be interpreted as the set of isomorphism classes of topological principal bundles over
can be interpreted as the set of isomorphism classes of topological principal bundles over  with structure group
with structure group 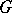 . Similarly one obtains a classification of smooth and holomorphic principal bundles. In a similar fashion one defines the non-Abelian cohomology for a site; for an interpretation see Principal
. Similarly one obtains a classification of smooth and holomorphic principal bundles. In a similar fashion one defines the non-Abelian cohomology for a site; for an interpretation see Principal 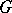 -object.
-object.
2) Let 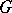 be a group and let
be a group and let  be a (not necessarily Abelian)
be a (not necessarily Abelian) 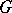 -group, i.e. an operator group with group of operators
-group, i.e. an operator group with group of operators  . Denote the action of an operator
. Denote the action of an operator  on an element
on an element 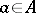 by
by 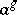 . Define a complex
. Define a complex 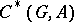 by the formulas
by the formulas
The group 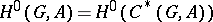 is the subgroup
is the subgroup 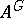 of
of  -fixed points in
-fixed points in  , while
, while 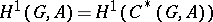 is the set of equivalence classes of crossed homomorphisms
is the set of equivalence classes of crossed homomorphisms 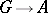 , interpreted as the set of isomorphism classes of principal homogeneous spaces (cf. Principal homogeneous space) over
, interpreted as the set of isomorphism classes of principal homogeneous spaces (cf. Principal homogeneous space) over 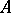 . For applications and actual computations of non-Abelian cohomology groups see Galois cohomology. Analogous definitions yield the non-Abelian cohomology of categories and semi-groups.
. For applications and actual computations of non-Abelian cohomology groups see Galois cohomology. Analogous definitions yield the non-Abelian cohomology of categories and semi-groups.
3) Let  be a smooth manifold,
be a smooth manifold, 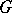 a Lie group and
a Lie group and 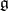 the Lie algebra of
the Lie algebra of  . The non-Abelian de Rham complex
. The non-Abelian de Rham complex 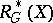 is defined as follows:
is defined as follows: 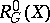 is the group of all smooth functions
is the group of all smooth functions 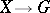 ;
; 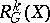 ,
,  , is the space of exterior
, is the space of exterior 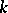 -forms on
-forms on 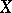 with values in
with values in 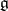 ;
;
The set 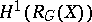 is the set of classes of totally-integrable equations of the form
is the set of classes of totally-integrable equations of the form 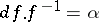 ,
, 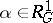 , modulo gauge transformations. An analogue of the de Rham theorem provides an interpretation of this set as a subset of the set
, modulo gauge transformations. An analogue of the de Rham theorem provides an interpretation of this set as a subset of the set 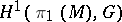 of conjugacy classes of homomorphisms
of conjugacy classes of homomorphisms 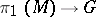 . In the case of a complex manifold
. In the case of a complex manifold 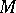 and a complex Lie group
and a complex Lie group 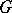 , one again defines a non-Abelian holomorphic de Rham complex and a non-Abelian Dolbeault complex, which are intimately connected with the problem of classifying holomorphic bundles [3]. Non-Abelian complexes of differential forms are also an important tool in the theory of pseudo-group structures on manifolds.
, one again defines a non-Abelian holomorphic de Rham complex and a non-Abelian Dolbeault complex, which are intimately connected with the problem of classifying holomorphic bundles [3]. Non-Abelian complexes of differential forms are also an important tool in the theory of pseudo-group structures on manifolds.
For each subcomplex of a non-Abelian cochain complex there is an associated exact cohomology sequence. For example, for the complex 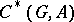 of Example 2 and its subcomplex
of Example 2 and its subcomplex 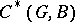 , where
, where  is a
is a 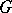 -invariant subgroup of
-invariant subgroup of  , this sequence is
, this sequence is
If 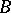 is a normal subgroup of
is a normal subgroup of 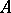 , the sequence can be continued up to the term
, the sequence can be continued up to the term  , and if
, and if 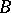 is in the centre it can be continued to
is in the centre it can be continued to 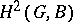 . This sequence is exact in the category of sets with a distinguished point. In addition, a tool is available ( "twisted" cochain complexes) for describing the pre-images of all — not only the distinguished — elements (see [1], [6], [3]). One can also construct a spectral sequence related to a double non-Abelian complex, and the corresponding exact boundary sequence.
. This sequence is exact in the category of sets with a distinguished point. In addition, a tool is available ( "twisted" cochain complexes) for describing the pre-images of all — not only the distinguished — elements (see [1], [6], [3]). One can also construct a spectral sequence related to a double non-Abelian complex, and the corresponding exact boundary sequence.
Apart from the 0- and 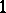 -dimensional non-Abelian cohomology groups just described, there are also
-dimensional non-Abelian cohomology groups just described, there are also  -dimensional examples. A classical example is the
-dimensional examples. A classical example is the  -dimensional cohomology of a group
-dimensional cohomology of a group 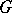 with coefficients in a group
with coefficients in a group 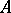 ; the definition is as follows. Let
; the definition is as follows. Let 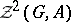 denote the set of all pairs
denote the set of all pairs 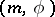 , where
, where 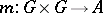 ,
, 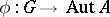 are mappings such that
are mappings such that
here 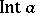 is the inner automorphism generated by the element
is the inner automorphism generated by the element 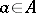 . Define an equivalence relation in
. Define an equivalence relation in 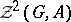 by putting
by putting 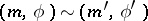 if there is a mapping
if there is a mapping 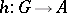 such that
such that
and
The equivalence classes thus obtained are the elements of the cohomology set 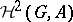 . They are in one-to-one correspondence with the equivalence classes of extensions of
. They are in one-to-one correspondence with the equivalence classes of extensions of 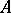 by
by 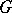 (see Extension of a group).
(see Extension of a group).
The correspondence 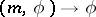 gives a mapping
gives a mapping 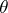 of the set
of the set  into the set of all homomorphisms
into the set of all homomorphisms
let 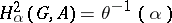 for
for 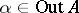 . If one fixes
. If one fixes 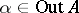 , the centre
, the centre 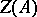 of
of 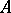 takes on the structure of a
takes on the structure of a 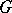 -module and so the cohomology groups
-module and so the cohomology groups 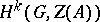 are defined. It turns out that
are defined. It turns out that 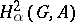 is non-empty if and only if a certain class in
is non-empty if and only if a certain class in 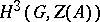 is trivial. Moreover, under this condition the group
is trivial. Moreover, under this condition the group 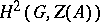 acts simplely transitively on the set
acts simplely transitively on the set  .
.
This definition of a two-dimensional cohomology can be generalized, carrying it over to sites (see [2], where the applications of this concept are also presented). A general algebraic scheme that yields a two-dimensional cohomology is outlined in [4]; just as in the special case described above, computation of two-dimensional cohomology reduces to the computation of one-dimensional non-Abelian and ordinary Abelian cohomology.
References
| [1] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) |
| [2] | J. Giraud, "Cohomologie non abélienne" , Springer (1971) |
| [3] | A.L. Onishchik, "Some concepts and applications of the theory of non-Abelian cohomology" Trans. Moscow Math. Soc. , 17 (1979) pp. 49–98 Trudy Moskov. Mat. Obshch. , 17 (1967) pp. 45–88 |
| [4] | A.K. Tolpygo, "Two-dimensional cohomologies and the spectral sequence in the nonabelian theory" Selecta Math. Sov. , 6 (1987) pp. 177–197 |
| [5] | P. Dedecker, "Three-dimensional nonabelian cohomology for groups" , Category theory, homology theory and their applications (Battelle Inst. Conf.) , 2 , Springer (1968) pp. 32–64 |
| [6] | J. Frenkel, "Cohomology non abélienne et espaces fibrés" Bull. Soc. Math. France , 85 : 2 (1957) pp. 135–220 |
| [7] | H. Goldschmidt, "The integrability problem for Lie equations" Bull. Amer. Math. Soc. , 84 : 4 (1978) pp. 531–546 |
| [8] | T.A. Springer, "Nonabelian 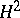 in Galois cohomology" A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 164–182 in Galois cohomology" A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 164–182 |
 ,
, 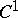 be groups, let
be groups, let  be a set with a distinguished point
be a set with a distinguished point  , let
, let  be the holomorph of
be the holomorph of  (i.e. the semi-direct product of
(i.e. the semi-direct product of  and
and 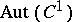 ; cf. also Holomorph of a group), and let
; cf. also Holomorph of a group), and let  be the group of permutations of
be the group of permutations of  that leave
that leave  fixed. Then a non-Abelian cochain complex is a collection
fixed. Then a non-Abelian cochain complex is a collection
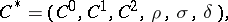
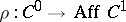 ,
, 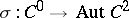 are homomorphisms and
are homomorphisms and  is a mapping such that
is a mapping such that
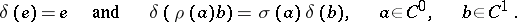
 -dimensional cohomology group by
-dimensional cohomology group by
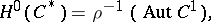
 -dimensional cohomology set (with distinguished point) by
-dimensional cohomology set (with distinguished point) by

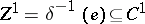 and the factorization is modulo the action
and the factorization is modulo the action  of the group
of the group  .
.
 be a topological space with a sheaf of groups
be a topological space with a sheaf of groups  , and let
, and let  be a covering of
be a covering of  ; one then has the Čech complex
; one then has the Čech complex
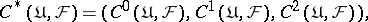
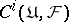 are defined as in the Abelian case (see Cohomology),
are defined as in the Abelian case (see Cohomology),
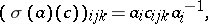
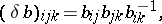
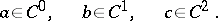
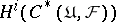 ,
,  , the cohomology
, the cohomology 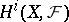 ,
, 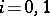 , of the space
, of the space 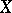 with coefficients in
with coefficients in 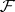 . Under these conditions,
. Under these conditions, 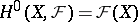 . If
. If 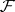 is the sheaf of germs of continuous mappings with values in a topological group
is the sheaf of germs of continuous mappings with values in a topological group 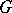 , then
, then  can be interpreted as the set of isomorphism classes of topological principal bundles over
can be interpreted as the set of isomorphism classes of topological principal bundles over  with structure group
with structure group 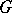 . Similarly one obtains a classification of smooth and holomorphic principal bundles. In a similar fashion one defines the non-Abelian cohomology for a site; for an interpretation see Principal
. Similarly one obtains a classification of smooth and holomorphic principal bundles. In a similar fashion one defines the non-Abelian cohomology for a site; for an interpretation see Principal 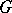 -object.
-object.
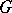 be a group and let
be a group and let  be a (not necessarily Abelian)
be a (not necessarily Abelian) 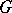 -group, i.e. an operator group with group of operators
-group, i.e. an operator group with group of operators  . Denote the action of an operator
. Denote the action of an operator  on an element
on an element 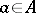 by
by 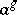 . Define a complex
. Define a complex 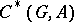 by the formulas
by the formulas
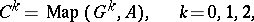
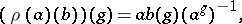
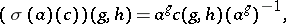


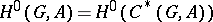 is the subgroup
is the subgroup 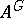 of
of  -fixed points in
-fixed points in  , while
, while 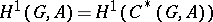 is the set of equivalence classes of crossed homomorphisms
is the set of equivalence classes of crossed homomorphisms 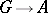 , interpreted as the set of isomorphism classes of principal homogeneous spaces (cf. Principal homogeneous space) over
, interpreted as the set of isomorphism classes of principal homogeneous spaces (cf. Principal homogeneous space) over 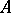 . For applications and actual computations of non-Abelian cohomology groups see Galois cohomology. Analogous definitions yield the non-Abelian cohomology of categories and semi-groups.
. For applications and actual computations of non-Abelian cohomology groups see Galois cohomology. Analogous definitions yield the non-Abelian cohomology of categories and semi-groups.
 be a smooth manifold,
be a smooth manifold, 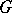 a Lie group and
a Lie group and 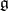 the Lie algebra of
the Lie algebra of  . The non-Abelian de Rham complex
. The non-Abelian de Rham complex 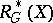 is defined as follows:
is defined as follows: 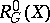 is the group of all smooth functions
is the group of all smooth functions 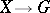 ;
; 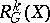 ,
,  , is the space of exterior
, is the space of exterior 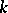 -forms on
-forms on 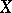 with values in
with values in 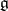 ;
;
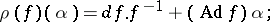
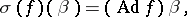
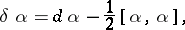
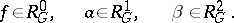
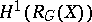 is the set of classes of totally-integrable equations of the form
is the set of classes of totally-integrable equations of the form 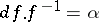 ,
, 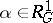 , modulo gauge transformations. An analogue of the de Rham theorem provides an interpretation of this set as a subset of the set
, modulo gauge transformations. An analogue of the de Rham theorem provides an interpretation of this set as a subset of the set 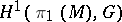 of conjugacy classes of homomorphisms
of conjugacy classes of homomorphisms 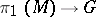 . In the case of a complex manifold
. In the case of a complex manifold 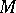 and a complex Lie group
and a complex Lie group 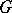 , one again defines a non-Abelian holomorphic de Rham complex and a non-Abelian Dolbeault complex, which are intimately connected with the problem of classifying holomorphic bundles [3]. Non-Abelian complexes of differential forms are also an important tool in the theory of pseudo-group structures on manifolds.
, one again defines a non-Abelian holomorphic de Rham complex and a non-Abelian Dolbeault complex, which are intimately connected with the problem of classifying holomorphic bundles [3]. Non-Abelian complexes of differential forms are also an important tool in the theory of pseudo-group structures on manifolds.
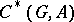 of Example 2 and its subcomplex
of Example 2 and its subcomplex 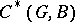 , where
, where  is a
is a 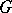 -invariant subgroup of
-invariant subgroup of  , this sequence is
, this sequence is

 is a normal subgroup of
is a normal subgroup of  , the sequence can be continued up to the term
, the sequence can be continued up to the term  , and if
, and if  is in the centre it can be continued to
is in the centre it can be continued to 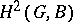 . This sequence is exact in the category of sets with a distinguished point. In addition, a tool is available ( "twisted" cochain complexes) for describing the pre-images of all — not only the distinguished — elements (see [1], [6], [3]). One can also construct a spectral sequence related to a double non-Abelian complex, and the corresponding exact boundary sequence.
. This sequence is exact in the category of sets with a distinguished point. In addition, a tool is available ( "twisted" cochain complexes) for describing the pre-images of all — not only the distinguished — elements (see [1], [6], [3]). One can also construct a spectral sequence related to a double non-Abelian complex, and the corresponding exact boundary sequence.
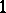 -dimensional non-Abelian cohomology groups just described, there are also
-dimensional non-Abelian cohomology groups just described, there are also  -dimensional examples. A classical example is the
-dimensional examples. A classical example is the  -dimensional cohomology of a group
-dimensional cohomology of a group 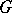 with coefficients in a group
with coefficients in a group 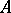 ; the definition is as follows. Let
; the definition is as follows. Let 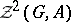 denote the set of all pairs
denote the set of all pairs 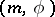 , where
, where 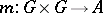 ,
, 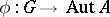 are mappings such that
are mappings such that
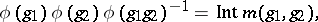
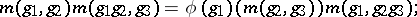
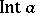 is the inner automorphism generated by the element
is the inner automorphism generated by the element 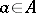 . Define an equivalence relation in
. Define an equivalence relation in 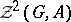 by putting
by putting 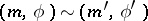 if there is a mapping
if there is a mapping 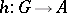 such that
such that
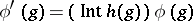
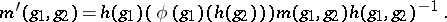
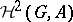 . They are in one-to-one correspondence with the equivalence classes of extensions of
. They are in one-to-one correspondence with the equivalence classes of extensions of 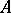 by
by 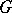 (see Extension of a group).
(see Extension of a group).
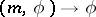 gives a mapping
gives a mapping 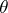 of the set
of the set  into the set of all homomorphisms
into the set of all homomorphisms
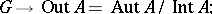
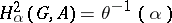 for
for 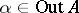 . If one fixes
. If one fixes 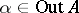 , the centre
, the centre 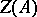 of
of 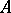 takes on the structure of a
takes on the structure of a 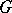 -module and so the cohomology groups
-module and so the cohomology groups 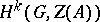 are defined. It turns out that
are defined. It turns out that 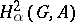 is non-empty if and only if a certain class in
is non-empty if and only if a certain class in 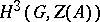 is trivial. Moreover, under this condition the group
is trivial. Moreover, under this condition the group 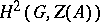 acts simplely transitively on the set
acts simplely transitively on the set  .
.
 in Galois cohomology" A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 164–182
in Galois cohomology" A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 164–182