Lie group, supersolvable

triangular Lie group

A connected real Lie group for which the eigen values of the operators of adjoint representation (cf. Adjoint representation of a Lie group) are real for any element .

A connected Lie group is supersolvable if and only if its Lie algebra is supersolvable, so a number of properties of the class of supersolvable Lie groups are parallel with properties of supersolvable Lie algebras (cf. Lie algebra, supersolvable).

The following fixed-point theorem is true for a supersolvable Lie group [2]: Any supersolvable Lie subgroup of a projective group has a fixed point in every -invariant closed subset of the real projective space. There are also other analogues of properties of complex solvable Lie groups. An arbitrary connected Lie group has maximal connected supersolvable Lie groups , and they are all conjugate in 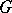(see [2]). To study the structure of real semi-simple Lie groups, the subgroup 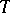is often used as the real analogue of a Borel subgroup.

A simply-connected supersolvable Lie group can be isomorphically imbedded in the group of real upper-triangular matrices over 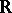with positive diagonal elements (which is itself supersolvable).

References

[1]	A. Borel, "Linear algebraic groups" , Benjamin (1969)
[2]	E.B. Vinberg, "The Morozov–Borel theorem for real Lie groups" Soviet Math. Dokl. , 2 (1961) pp. 1416–1419 Dokl. Akad. Nauk SSSR , 141 (1961) pp. 270–273

Comments

In [1] the phrase "trigonalizable Lie grouptrigonalizable Lie group" is used instead of supersolvable. The literal translation of the Russian expression is fully-solvable Lie group.