Cartan subalgebra
of a finite-dimensional Lie algebra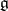 
over a field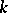 
A nilpotent subalgebra of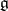 
which is equal to its normalizer in 
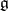. For example, if 
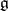is the Lie algebra of all complex square matrices of a fixed order, then the subalgebra of all diagonal matrices is a Cartan subalgebra in 
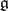. A Cartan subalgebra can also be defined as a nilpotent subalgebra 
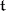in 
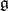which is equal to its Fitting null-component (cf. Weight of a representation of a Lie algebra)
 |
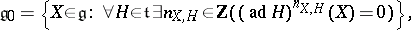where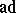 
denotes the adjoint representation (cf. Lie algebra) of 
.
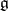Suppose further that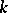 
is of characteristic zero. Then for any regular element 
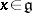, the set 
of all elements of 
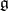which are annihilated by powers of 
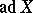is a Cartan subalgebra of 
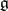, and every Cartan subalgebra of 
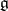has the form 
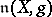for some suitable regular element 
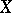. Each regular element belongs to one and only one Cartan subalgebra. The dimension of all the Cartan subalgebras of 
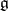are the same and are equal to the rank of 
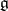. The image of a Cartan subalgebra under a surjective homomorphism of Lie algebras is a Cartan subalgebra. If 
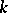is algebraically closed, then all Cartan subalgebras of 
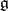are conjugate; more precisely, they can be transformed into another by operators of the algebraic group 
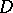of automorphisms of 
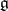whose Lie algebra is the commutator subalgebra of 
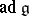. If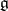 
is solvable, then the above assertion holds without the hypothesis that 
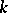be algebraically closed.
Let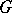 
be either a connected linear algebraic group over an algebraically closed field 
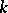of characteristic zero, or a connected Lie group, and let 
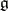be its Lie algebra. Then a subalgebra 
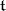of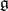 
is a Cartan subalgebra if and only if it is the Lie algebra of a Cartan subgroup of 
.
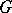Let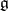 
be a subalgebra of the Lie algebra 
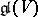of all endomorphisms of a finite-dimensional vector space 
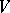over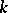 
, and let 
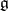be the smallest algebraic Lie algebra in 
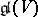containing 
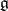(cf. Lie algebra, algebraic). If 
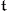is a Cartan subalgebra of 
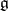, then 
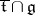is a Cartan subalgebra of 
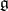, and if 
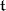is a Cartan subalgebra of 
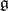and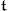 
is the smallest algebraic subalgebra of 
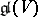containing 
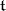, then 
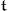is a Cartan subalgebra of 
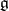and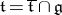 
.
Let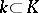 
be a field extension. A subalgebra 
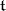of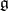 
is a Cartan subalgebra if and only if 
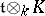is a Cartan subalgebra of 
.
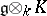Cartan subalgebras play an especially important role when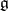 
is a semi-simple Lie algebra (this was used by E. Cartan [1]). In this case, every Cartan subalgebra 
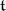of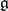 
is Abelian and consists of semi-simple elements (see Jordan decomposition), and the restriction of the Killing form to 
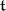is non-singular.
References
| [1] | E. Cartan, "Sur la structure des groupes de transformations finis et continus" , Paris (1894) |
| [2] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [3] | C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946) |
| [4] | , Theórie des algèbres de Lie. Topologie des groupes de Lie , Sem. S. Lie , Ie année 1954–1955 , Ecole Norm. Sup. (1955) |
Comments
An element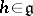 
is called regular if the dimension of the Fitting null-component of the endomorphism 
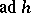of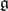 
is minimal. "Almost-all" elements of 
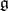are regular in the sense that the condition of being regular defines a Zariski-open subset. The result that the Fitting null-component of 
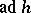for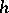 
regular is a Cartan subalgebra holds for finite-dimensional Lie algebras over any infinite field [a4], p. 59.
References
| [a1] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [a2] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 |
| [a3] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [a4] | N. Jacobson, "Lie algebras" , Dover, reprint (1979) ((also: Dover, reprint, 1979)) |
Cartan subalgebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartan_subalgebra&oldid=21820