Measure-preserving transformation

of a measure space .

A measurable mapping such that for every ; is called an invariant measure for . A measurable mapping between measure spaces and such that for every is usually called a measure-preserving mapping. A surjective measure-preserving transformation 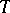of a measure space 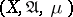, i.e., 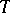maps 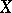onto itself, is often called an endomorphism of ; an endomorphism which is bijective and whose inverse is also measure preserving is called an automorphism of .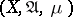

Measure-preserving transformations arise, for example, in the study of classical dynamical systems (cf. (measurable) Cascade; Measurable flow). In that case the transformation is first obtained as a continuous (or smooth) transformation of some, often compact, topological space (or manifold), and the existence of an invariant measure is proved. An example is Liouville's theorem for a Hamiltonian system (cf. also Liouville theorems).

For further information and references see Ergodic theory.