Permutation of a set

A one-to-one mapping of a set onto itself. The term permutation is used mainly for a finite set 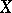. In that case it is convenient to assume that 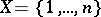and to write the permutation in the form

(*)

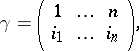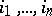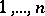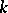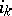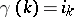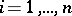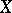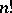where is a certain permutation of the numbers . The notation (*) means that transforms the number into , i.e. (one writes also ) for . The number of different permutations of a set with is equal to . The product of the permutations 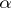and 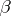of a set 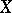is defined as the successive application of the mappings 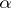and 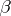, and is given by the formula 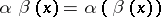for all 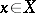. The set of all permutations of 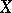forms a group with respect to this multiplication, called the symmetric group. Any subgroup of a symmetric group is called a permutation group.

The symmetric group of permutations of a set 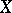is denoted by 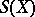, and it contains as a subgroup 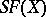, the group consisting of those permutations 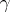which displace only a finite subset of elements (i.e. 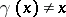only for a finite set of elements 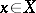). If 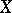is finite and consists of elements, the symmetric group is denoted by .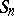

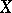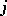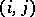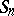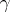A transposition is a permutation of that displaces only two elements and ; it is denoted by . In there are precisely transpositions. Any permutation in 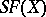can be written as a product of transpositions. In particular, each permutation in 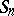is a product of transpositions. A permutation can be written as a product of transpositions in many ways. However, for a given 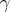the parity of the number of factors in a decomposition of 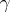into transpositions is independent of the method of decomposing it. A permutation representable as a product of an even number of transpositions is called even, while one that decomposes as a product of an odd number of transpositions is called odd. In 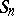there are 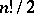even permutations and the same number of odd ones. If a permutation 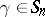is written in the form (*), its parity coincides with the parity of the number of inversions in the permutation 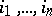, i.e. it is equal to the number of pairs 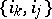such that 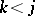, 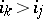. A transposition is clearly an odd permutation. Composing a permutation with a single transposition alters the parity of the number of inversions. The product of two even permutations, and also of two odd ones, is an even permutation, while the product of an even and an odd permutation (in either order) is odd. The even permutations constitute a normal subgroup 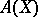in the group 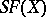, called the alternating group. 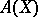For , the subgroup is denoted by .

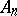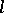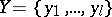A cycle of length is a permutation of a finite set such that

A finite cycle is denoted by 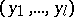. An infinite cycle is a permutation of a countable set, of the form

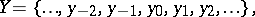where for any integer 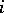, 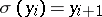. The symbol for an infinite cycle is:

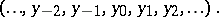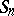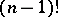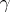A cycle of length 2 is a transposition. The group contains cycles of length . For any permutation from 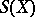there exists a decomposition of 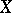into non-intersecting subsets such that on each of them 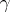acts as a cycle. The finite subsets in this decomposition take the form

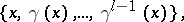where 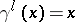, while the infinite ones take the form

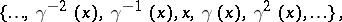where 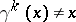for 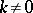. The cycles induced by 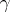on the subsets of the decomposition are called disjoint cycles of the permutation 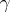. For example, 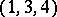and 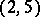are disjoint cycles of the permutation

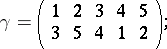and 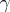is written in the form

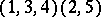as the product of its disjoint cycles. In general, if 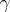is not the identity permutation and has only a finite number of cycles of length greater than one, then 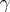is the product of such cycles. In particular, each non-identity permutation from 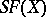is the product of its disjoint cycles of length greater than one. The order of a permutation 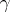from 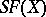, i.e. the order of the cyclic group 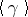, is equal to the lowest common multiple of the lengths of its disjoint cycles.

From the disjoint cycles of a given permutation one can obtain the disjoint cycles of any permutation conjugate with it (cf. Conjugate elements). For example, if

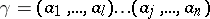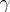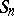is the product of the disjoint cycles of the permutation from , if 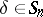and if 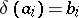, , 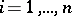then

is the decomposition of the permutation 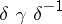as a product of disjoint cycles. Two permutations of the group 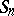are conjugate in 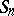if and only if they have the same number of disjoint cycles of each length.

Let 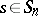and let 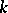be the number of independent cycles of , including cycles of length 1. Then the difference 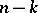is called the decrement of the permutation . The least number of factors in a decomposition of the permutation as a product of transpositions coincides with its decrement. The parity of a permutation coincides with the parity of its decrement.

Permutations arose originally in combinatorics in the 18th century. At the end of the 18th century, J.L. Lagrange applied them in his research on the solvability of algebraic equations by radicals. A.L. Cauchy gave much attention to this topic, and was responsible, in particular, for the idea of expressing a permutation as a product of cycles. Research on the group properties of permutations has been carried out by N.H. Abel and, particularly, by E. Galois. See Galois theory and Permutation group.

References

[1]	C. Jordan, "Traité des substitutions et des équations algébriques" , Paris (1957)
[2]	A.I. Kostrikin, "Introduction to algebra" , Springer (1982) (Translated from Russian)
[3]	A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian)
[4]	M. Hall, "Group theory" , Macmillan (1959)

Comments

In the notation 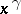, the expression 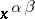is to be read as 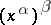, i.e. first 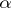, then .

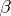References

[a1]	M. Suzuki, "Group theory" , 1–2 , Springer (1986)